SDEs for Financial Modelling - Concise Notes
MATH70141
PDFs
Table of contents
Probability and SDEs
Definition 1 ($\Sigma$ - sample space). It is the set of all elementary outcomes of a random experiment
Definition 2 ($\mathcal{F}$ - sigma-field ). Also denoted by $\sigma$-field, it is a collection of subsets of $\Sigma$ that satisfies the following properties:
$\emptyset \in \mathcal{F}$ and $\mathcal{F}$
If $A \in \mathcal{F}$, then $A^{c} \in \mathcal{F}$
If $A_{1}, A_{2}, \ldots \in \mathcal{F}$, then $\bigcup_{i=1}^{\infty} A_{i} \in \mathcal{F}$, i.e. $\mathcal{F}$ is closed under countable unions
Trivial $\sigma$-filed given by $\mathcal{F} = {\Omega ,\varnothing }$
Power set of $\Sigma$ is the largest $\sigma$-field, denoted by $\mathcal{P}(\Sigma )$ containing all possible subsets of $\Sigma$
Definition 3 (Borel set). The smallest $\sigma$-field that contains all open sets in $\mathbb{R}$ is called the Borel $\sigma$-field, denoted by $\mathcal{B}(\mathbb{R})$
Definition 4 (Borel $\sigma$-field). $\sigma$-Field generated by open sets in $\mathbb{R}$ is called the Borel $\sigma$-field, denoted by $\mathcal{B}(\mathbb{R})$, containing all open, closed, half-open, half-closed, and countable unions of these sets. It is the smallest $\sigma$-field that contains all open sets in $\mathbb{R}$ \(\mathcal{B}(\mathbb{R}) = \sigma \left( \{ (a,b) \mid a,b \in \mathbb{R}\} \right)\)
Definition 5 (Probability measure). A function $P: \mathcal{F} \to [0,1]$ is called a probability measure if it satisfies the following properties:
$P(\Omega ) = 1,\ P(\varnothing ) = 0$
$P(A) \geq 0$ for all $A \in \mathcal{F}$
If $A_{1}, A_{2}, \ldots \in \mathcal{F}$ are pairwise disjoint, then $P\left( \bigcup_{i=1}^{\infty} A_{i} \right) = \sum_{i=1}^{\infty} P(A_{i})$
Definition 6 (Random variable). A random variable is a function $X: \Omega \to \mathbb{R}$ that maps the sample space to the real numbers.
It is measurable if for all $B \in \mathcal{B}(\mathbb{R})$, the set $X^{-1}(\mathcal{B} ) = { \omega \in \Omega \mid X(\omega ) \in B } \in \mathcal{F}$
Definition 7 (Cumuative distribution function). The cumulative distribution function (CDF) of a random variable $X$ is defined as $F_{X}(x) = P(X \leq x)$ for all $x \in \mathbb{R}$ \(P(X^{-1} ((-\infty , x])) = P(\{\omega \in \Omega \mid X(\omega ) \leq x\}) = F_{X}(x)\)
Definition 8 (Probability density function). If there exists a function $f_{X}: \mathbb{R}\to \mathbb{R}$ such that for all $x \in \mathbb{R}$, $F_{X}(x) = \int_{-\infty}^{x} f_{X}(y)dy$, then $f_{X}$ is called the probability density function (pdf) of $X$
Or equivalently if the CDF differentiable the pdf is: $f_{X}(x) = \frac{d}{dx}F_{X}(x)$
Definition 9 (Expectation). The expectation of a random variable $X$ is defined as: \(\begin{aligned} E[X] &= \int_{\Omega } X(\omega )dP(\omega )\\ &= \int_{\mathbb{R}} y dF_{x}(y)\\ &= \int_{\mathbb{R}} y f_{X}(y)dy \end{aligned}\)
Definition 10 (Variance). The variance of a random variable $X$ is defined as: \(\begin{aligned} Var(X) &= E[(X - E[X])^{2}]\\ &= E[X^{2}] - E[X]^{2} \end{aligned}\)
Proposition 11 (Properties of expectation). Let $X, Y$ be random variables and $a, b \in \mathbb{R}$, then:
$E[aX + bY] = aE[X] + bE[Y]$
If $X \geq 0$, then $E[X] \geq 0$
If $X \geq Y$, then $E[X] \geq E[Y]$
Proposition 12 (Properties of variance). Let $X, Y$ be random variables and $a, b \in \mathbb{R}$, then:
$Var(aX + bY) = a^{2}Var(X) + b^{2}Var(Y) + 2abCov(X,Y)$
$Var(X) \geq 0$
If $X \geq 0$, then $Var(X) \geq 0$
If $X \geq Y$, then $Var(X) \geq Var(Y)$
Definition 13 (Moment generating function). The moment generating function (mgf) of a random variable $X$ is defined as: \(M_{X}(t) = E[e^{tX}]\)
We have that
\[\frac{d^{n}}{dt^{n}}M_{X}(t) = E[X^{n}e^{tX}]\]Definition 14 (Characteristic function). Not all random variables have a MGF, we instead have the characteristic function (cf) of a random variable $X$ is defined as: \(\phi_{X}(t) = E[e^{itX}]\)
Definition 15 (Independence). Two random variables $X, Y$ are independent if for all $A, B \in \mathcal{B}(\mathbb{R})$, we have that:
\[P(X \in A, Y \in B) = P(X \in A)P(Y \in B)\]and denoted by $X \perp Y$ We also have that \(\begin{aligned} E[XY] &= E[X]E[Y]\\ Var(X + Y) &= Var(X) + Var(Y) \end{aligned}\)
Definition 16 (Covariance). The covariance of two random variables $X, Y$ is defined as: \(Cov(X,Y) = E[(X - E[X])(Y - E[Y])] = E[XY] - E[X]E[Y]\)
Definition 17 (Correlation). The correlation of two random variables $X, Y$ is defined as:
\[Corr(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}\]We have that $-1 \leq Corr(X,Y) \leq 1$. For random variables $X_1, X_2$ with $X_2 = aX_1 + b$, we have that $Corr(X_1, X_2) = 1$ or $-1$ depending on the sign of $a$. Can define a correlation or covariance matrix for a vector of random variables $\mathbf{X} = (X_{1}, X_{2}, \ldots , X_{n})$ as the matrix of all pairwise correlations or covariances
Theorem 18 (Central Limit Theorem). *Let $X_{1}, X_{2}, \ldots$ be a sequence of i.i.d. random variables with mean $\mu$ and variance $\sigma^{2}$. We have sample mean defined as $\overline{X}_{n}$
\[\begin{aligned} \overline{X}_{n} &= \frac{1}{n}\sum_{i=1}^{n} X_{i}\\ \sqrt{n}\frac{\overline{X}_{n} - \mu }{\sigma} &\xrightarrow{n \uparrow \infty } N(0, 1) \end{aligned}\]Example 19. Take $X \sim N(\mu ,\sigma^{2})$, then we have that:
\[E[(X-\mu )^n] = \begin{cases} 0 & \text{if } n \text{ is odd}\\ \sigma^{n}n!! & \text{if } n \text{ is even} \end{cases}\]where $n!!$ is the double factorial defined as $n!! = n(n-2)(n-4)\ldots$
Definition 20 (Multivariate random variable). A multivariate random variable is a vector of random variables $\mathbf{X} = (X_{1}, X_{2}, \ldots , X_{n})$. The joint distribution of $\mathbf{X}$ is defined as: \(F_{\mathbf{X}}(x_{1}, x_{2}, \ldots , x_{n}) = P(X_{1} \leq x_{1}, X_{2} \leq x_{2}, \ldots , X_{n} \leq x_{n})\)
With the PDF defined as:
\[f_{\mathbf{X}}(x_{1}, x_{2}, \ldots , x_{n}) = \frac{\partial^{n}}{\partial x_{1} \partial x_{2} \ldots \partial x_{n}}F_{\mathbf{X}}(x_{1}, x_{2}, \ldots , x_{n})\]Definition 21 (Multivariate Normal). We define for dimension $n$. Let $\mu = [\mu_1, \mu_2, \cdots, \mu_n]$ be the vector for the means and let $V$ be a covariance matrix, $V_{i,j} = \sigma_i \sigma_j \rho_{i,j}$.
We say that $X$ follows a multivariate normal distribution in dimension $n$ and we write $X = [X_1, \cdots, X_n] \sim N(\mu, V) \sim N((\mu_i){i=1,\ldots,n}, (\sigma_i \sigma_j \rho{i,j})_{i,j=1\ldots n})$ if
\[p_X(y) = p_{X_1,\ldots,X_n}(y_1, \cdots, y_n) = \frac{(2\pi)^{-n/2}}{\sqrt{\det(V)}} \exp\left(-\frac{1}{2}(y - \mu)^TV^{-1}(y - \mu)\right)\]Definition 22 (Convergence of Random Variables). Let $X, X_{1}, X_{2}, \ldots$ be random variables, then we have the following types of convergence:
Almost sure convergence: $X_{n} \xrightarrow{a.s.} X$ if $P(\lim_{n \to \infty} X_{n} = X) = 1$
$L^{p}$ convergence: $X_{n} \xrightarrow{L^{p}} X$ if $E[|X_{n} - X|^{p}] \to 0$ as $n \to \infty$
Making sure that $E[|X_{n}|^{p}] < \infty$ for all $n \in \mathbb{N}$
Convergence in mean square: $X_{n} \xrightarrow{m.s.} X$ if $E[(X_{n} - X)^{2}] \to 0$ as $n \to \infty$
Special case of $L^{p}$ convergence for $p = 2$
Convergence in probability: $X_{n} \xrightarrow{p} X$ if for all $\epsilon > 0$, $P(|X_{n} - X| > \epsilon ) \to 0$ as $n \to \infty$
Weak convergence or convergence in distribution: $X_{n} \xrightarrow{d} X$ if $F_{X_{n}}(x) \to F_{X}(x)$ for all $x \in \mathbb{R}$ where $F_{X_{n}}$ and $F_{X}$ are the CDFs of $X_{n}$ and $X$ respectively
Definition 23 (Stochastic Process). A stochastic process is a collection of random variables indexed by time, i.e. ${X_{t}}_{t \in T}$ where $T$ is the index set. We have the following types of stochastic processes:
Discrete-time: If $T = {0, 1, 2, \ldots }$
Continuous-time: If $T = [0, \infty )$
Markov process: If the future of the process depends only on the present state
Martingale: If the expected value of the process at time $t$ given all information up to time $s$ is equal to the value at time $s$
Definition 24 (Filtration). A filtration is a collection of $\sigma$-fields ${\mathcal{F}{t}}{t \in T}$ such that $\mathcal{F}{s} \subseteq \mathcal{F}{t}$ for all $s \leq t$. It represents the information available at time $t$
Definition 25 (Brownian Motion). A Brownian motion is a stochastic process ${W_{t}}_{t \geq 0}$ with the following properties:
$W_{0} = 0$
Continuous sample paths: $t \mapsto W_{t}(\omega)$
Independent Increments: For all $0 \leq s < t < u$, $W_{t} - W_{s}$ and $W_{u} - W_{t}$
Stationary Increments: Distribution of $W_{t+h} - W_{t}$ does not depend on $t$, but only on $h$ for $h > 0$
$W$ is Gaussian: $W_{t} \sim N(0, t)$ and $W_{t} - W_{s} \sim N(0, t-s)$ for all $0 \leq s < t$ under the probability measure $P$
Definition 26 (Ordinary Differential Equation). An ordinary differential equation (ODE) is an equation involving a function of one variable and its derivatives. It is of the form:
\[\frac{dX(t)}{dt} = f(X(t)),\quad X(0) = x_0\]where $y$ is the unknown function of $t$, and $f$ is a given function of $t$ and $y$
Can rewrite it as follows \(dX(t) = f(X(t))dt\)
Proposition 27 (Solution to Affine ODE). *The solution to an ODE of the following form for $A,B$ functions of time: \(\begin{aligned} \frac{dX(t)}{dt} &= B(t) - A(t)X(t)\\ X(t) &= \exp \left( -\int_{0}^{t} A(s)ds \right) \left( X(0) + \int_{0}^{t} B(u)\exp \left( \int_{0}^{u} A(s)ds \right)du \right) \end{aligned}\)
Definition 28 (Stochastic Differential Equation). A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process. It is of the form: \(dX(t) = \underbrace{f(X_{t})dt}_{\text{Local drift}} + \underbrace{\sigma(X_{t})}_{\text{Local } \sigma} \cdot \underbrace{dW_{t}}_{\text{Brownian motion}}\) where $X(t)$ is the unknown function of $t$, $f$ is the local drift, $\sigma$ is the local volatility, and $W_{t}$ is the Brownian motion process with $dW_{t} \sim N(0,dt)$
Problems:
Unbounded variation: Brownian motion has unbounded variation
Nowhere differentiable: Brownian motion is nowhere differentiable
So the integral of $dW_{t}$ is not well defined
Proposition 29 (Fixing the SDE). *Can’t use the standard Riemann-Stieltjes integral to solve the SDE as the Brownian motion is not of bounded variation.
\[P \left( \omega \in \Omega \mid \frac{dW_{t}}{dt} \text{ does not exist for any } t \right) = 1\]_In a Stiltjes integral one has \(\int_0^T \sigma(X_s) dW_s = \lim_{n \to \infty} \sum*{i=1}^n \sigma(X(t_i))(W*{t*{i+1}} - W*{t*i})\) for ANY choice $t_i \in [t_i, t*{i+1})$. We must carefully choose the partition $t_i$ to make the integral well defined.
We have 2 choices:_
*Ito’s Integral: \(\int_{0}^{T} \sigma(X_{s})dW_{s} = \lim_{n \to \infty} \sum_{i=1}^{n} \sigma(X(t_{i+1}))(W_{t_{i}} - W_{t_{i}})\) where $t_{i} = i\frac{T}{n}$ and $W_{t_{i+1}} - W_{t_{i}} \sim N(0, \frac{T}{n})$*
*Stratonovich Integral: \(\int_{0}^{T} \sigma(X_{s})\circ dW_{s} = \lim_{n \to \infty} \sum_{i=1}^{n} \frac{1}{2}(\sigma(X(t_{i})) + \sigma(X(t_{i+1}))) (W_{t_{i+1}} - W_{t_{i}})\)
Stratonovich Integral looks into the future to calculate the integral, while Ito’s Integral only uses current and past information.
If $\sigma(X{t})$ does not depend on $X_{t}$, then the two integrals are the same, we call this a Wiener Integral._
*We have the following property for Ito’s Integral: \(E \left[ \int_{0}^{T} \sigma(X_{s})dW_{s} \right] = 0\)
Proposition 30 (Ito’s Isometry). *We have that: \(E \left[ \left( \int_{0}^{t} \sigma(X_{s})dW_{s} \right)^{2} \right] = E \left[ \int_{0}^{t} \sigma(X_{s})^{2}ds \right]\)
Definition 31 (Adapted to Filtration). A stochastic process ${X_{t}}{t \in T}$ is adapted to a filtration ${\mathcal{F}{t}}{t \in T}$ if for all $t \in T$, $X{t}$ is $\mathcal{F}{t}$-measurable, i.e. $X{t}$ is known at time $t$
Theorem 32 (Existence and Uniqueness of Solutions). *Consider Ito SDE of the form:
\[dX(t) = \mu(t,X_{t})dt + \sigma(t,X_{t})dW_{t},\ X_0 = Z\]where $\mu, \sigma$ are Globally Lipschitz continuous and follow linear growth in $X$ and $\sigma \neq 0$. $Z$ a random variable independent $\sigma({W_{t}: t < T})$ and $E[Z^{2} ] < \infty$. Then there exists a unique global solution to the SDE on the interval $[0,T]$ that is adapted to the filtration generated by the Brownian motion, $\mathcal{F}_{t}^W$ and is square integrable.*
*Lipschitz continuity: A function $f: \mathbb{R}^{n} \to \mathbb{R}^{m}$ is Lipschitz continuous if there exists a constant $L > 0$ such that for all $x, y \in \mathbb{R}^{n}$, we have that: \(||f(x) - f(y)|| \leq L||x - y||\)
*Linear growth: A function $f: \mathbb{R}^{n} \to \mathbb{R}^{m}$ has linear growth if there exists a constant $K > 0$ such that for all $x \in \mathbb{R}^{n}$, we have that: \(||f(x)|| \leq K(1 + ||x||)\)
Definition 33 (Ito’s formula). Given \(dX_{t} = f(X_{t})dt + \sigma(X_{t})dW_{t}\)
we have that for a smooth function $\phi(t,x)$, the Ito’s formula is given by:
\[d \phi(t,X_{t}) = \frac{\partial \phi}{\partial t} dt + \frac{\partial \phi}{\partial x}dX_{t} + \frac{1}{2}\frac{\partial^{2} \phi}{\partial x^{2}}dX_{t}^{2}\]We have that:
$dtdt = 0$
$dW_{t}dW_{t} = dt$
$dtdW_{t} = 0$
Note for $V_{t}$ differentiable, we have that: \(dV_{t}dV_{t} = V^\prime (t) dt V^\prime (t) dt = V^\prime (t)^{2} \underbrace{dtdt}_{=0} = 0\)
Definition 34 (Quadratic Variation). The quadratic variation of a stochastic process ${X_{t}}_{t \in T}$ is defined as:
\[[X]_{t} = \lim_{n \to \infty} \sum_{i=1}^{n} (X_{t_{i+1}} - X_{t_{i}})^{2}\]where the limit is taken in the mean square sense. We have that:
\[[W]_{t} = t\]We have that for 2 independent Brownian motions $W, \widetilde{W}$, we have that:
\[[W, \widetilde{W}]_{t} = 0\]Now set $dW_t^{(1)} = dW_t^, dW_{t}^{(2)} = \rho dW_t + \sqrt{1- \rho^{2} }d \widetilde{W}_{t}$
\[d W_t^{(1)} dW_t^{(2)} = \rho dt\]Proposition 35 (Ito-Stratonovich Transformation). _We have that: \(dX_{t} = f(X*{t})dt + \sigma(X*{t})dW*{t} \rightarrow dX*{t} = \widetilde{f}(X*{t})dt + \sigma(X*{t})\circ dW*{t}\) where $\circ$ denotes the Stratonovich integral and $\widetilde{f} = f - \frac{1}{2}\sigma \frac{\partial \sigma}{\partial x}$. Here both integrals are equivalent. Note for $\sigma$ deterministic, the two integrals are the same.*
Definition 36 (Geometric Brownian Motion). A geometric Brownian motion is a stochastic process ${S_{t}}_{t \geq 0}$ with
\[dS_{t} = m_{t} S_{t}dt + \nu_{t} S_{t}dW_{t}\]where $m_{t}$ is the drift, $\nu_{t}$ is the volatility, and $W_{t}$ is the Brownian motion process. We have that:
\[S_{t} = S_{0} \exp \left( \underbrace{\int_{0}^{t} (m_{s} - \frac{1}{2}\nu_{s}^{2}) ds}_{M_{t}} + \underbrace{\int_{0}^{t} \nu_{s}dW_{s}}_{V_{t}^{2}} \right) = S_{0} e^{\mathcal{N}(M_{t}, V_{t}^{2})}\]: $E[S_{t}] = S_{0}\exp (\int_{0}^{t} m_{s}ds)$
: $Var(S_{t}) = S_{0}^{2}\exp (2\int_{0}^{t} m_{s}ds) \left( \exp (\int_{0}^{t} \nu_{s}^{2}ds) - 1 \right)$
Definition 37 (Arithmetic Brownian Motion). An arithmetic Brownian motion is a stochastic process ${S_{t}}_{t \geq 0}$ with
\[dS_{t} = \mu_{t}dt + \sigma_{t}dW_{t}\]where $\mu_{t}$ is the drift, $\sigma_{t}$ is the volatility, and $W_{t}$ is the Brownian motion process. We have that: \(S_{t} = S + \int_{0}^{t} \mu_{s}ds + \int_{0}^{t} \sigma_{s}dW_{s}\) We have that: \(S_{t}\sim N \left( S + \int_{0}^{t} \mu_{s}ds, \int_{0}^{t} \sigma_{s}^{2}ds \right)\)
Definition 38 (Ornstein-Uhlenbeck Process). An Ornstein-Uhlenbeck process is a stochastic process ${X_{t}}_{t \geq 0}$ with
\[dX_{t} = (b_{t}-a_{t}X_{t})dt + \sigma_{t}dW_{t}\]where $b_{t}$ is the drift, $a_{t}$ is the mean reversion, $\sigma_{t}$ is the volatility, and $W_{t}$ is the Brownian motion process. We have that:
\[X(t) = e^{-\int_0^t a(s)ds} \left[ \int_0^t \exp\left(\int_0^u a(s)ds\right) \left(b_u du + \sigma_u dW_u\right) + X(0) \right]\]Definition 39 (Vasicek Model). A special case of the Ornstein-Uhlenbeck process is the Vasicek model, where we have that:
\[dX_{t} = \kappa (\theta - X_{t})dt + \sigma dW_{t},\ x_0\]Where $\kappa$ is the mean reversion rate, $\theta$ is the long-term mean, $\sigma$ is the volatility, and $W_{t}$ is the Brownian motion process. We have $b(t) = \kappa \theta, a(t) = \kappa$ and $\sigma_{t} = \sigma$. Then: \(\begin{aligned} X(t) &= e^{-\kappa t}\left[ \exp (\kappa u) \left( \kappa \theta du + \sigma dW_{u} \right) + X(0) \right]\\ &= x_0 e^{-\kappa t} + \theta (1 - e^{-\kappa t}) + \sigma \int_0^t e^{-\kappa (t-u)}dW_u \end{aligned}\) We know $X_{t}$ will be Gaussian with mean $x_0 e^{-kt} + \theta (1 - e^{-\kappa t})$ and variance $\frac{\sigma^{2}}{2\kappa }(1 - e^{-2\kappa t})$
Definition 40 (CIR Model). A special case of the Ornstein-Uhlenbeck process \(\begin{aligned} \text{Vasicek:} &\quad dX_{t} = \kappa (\theta - X_{t})dt + \sigma dW_{t},\ x_0\\ \text{CIR:} &\quad dY_{t} = \kappa (\theta - Y_{t})dt + \sigma \sqrt{Y_{t}}dW_{t},\ x_0 \end{aligned}\) Where CIR is used to model interest rates $Y_{t} = r_{t}$ or volatility $Y_{t} = \nu_{t}$. Model can never be negative, but can be zero. We have the Feller condition for the CIR model to be positive: \(2\kappa \mu \geq \nu^{2}\) We have for both models that:
$\kappa$ : Mean reversion rate (speed of mean reversion rate)
$\theta$ : Long-term mean reversion level
$\sigma$ : Volatility
\(E[X_{t}] = E[Y_{t}] = x_0 e^{-\kappa t} + \theta (1 - e^{-\kappa t})\) \(Var(X_{t}) = \frac{\sigma^{2}}{2\kappa } (1 - e^{-2\kappa t}),\qquad Var(Y_{t}) = y_0 \frac{\sigma^{2}}{\kappa }(e^{-\kappa t} - e^{-2\kappa t}) + \frac{\theta \sigma^{2}}{2\kappa }(1 - e^{-\kappa t})^2\) \(\lim\limits_{t \to \infty} Var(X_{t}) = \frac{\sigma^{2} }{2k} \qquad \lim\limits_{t \to \infty} Var(Y_{t}) = \frac{\theta \sigma^{2}}{2\kappa }\)
Definition 41 (Product Rule for SDEs). Given two stochastic processes $X_{t}, Y_{t}$ with SDEs:
\[d(X_{t}Y_{t}) = X_{t}dY_{t} + Y_{t}dX_{t} + dX_{t}dY_{t}\]Last term computed with usual rules.
Definition 42 (Equivalent Measures). Say 2 measures $\mathbb{P}, \mathbb{Q}$ on $(\Sigma ,\mathcal{F} )$ are equivalent if they agree on which events have probability 0 or 1. We write $\mathbb{P} \sim \mathbb{Q}$
Definition 43 (Radon-Nikodym derivative). \(\mathbb{E}^{\mathbb{Q}}[X] = \int_{\Omega } Xd\mathbb{Q} = \int_{\Omega } X \frac{d\mathbb{Q}}{d\mathbb{P}}d\mathbb{P} = \mathbb{E}^{\mathbb{P}}[X \frac{d\mathbb{Q}}{d\mathbb{P}}]\)
Definition 44 (Girsanov’s Theorem). Define for all $t \in [0,T]$ \(\frac{d\mathbb{Q}}{d \mathbb{P}} \mid_{\mathcal{F}_{t}} := \exp \left[ -\frac{1}{2} \int_0^t \left(\frac{f^{\mathbb{Q}(X_{s}) - f^{\mathbb{P}}(X_{s})}}{\sigma(X_{s})}\right)^{2} ds + \int_0^t \frac{f^{\mathbb{Q}(X_{s}) - f^{\mathbb{P}}(X_{s})}}{\sigma(X_{s})} dW_{s}^{\mathbb{P}} \right]\) Then \(dX_{t} = f^{\mathbb{Q}}(X_{t})dt + \sigma(X_{t}) dW_{t}^{\mathbb{Q}}\)
Definition 45 (Poisson Process). A Poisson process is a counting process ${N_{t}}_{t \geq 0}$ with the following properties:
$N_{0} = 0$
All jumps are of size 1
Right continuity: $t \mapsto N_{t}(\omega )$ is right continuous
Independent increments: For all $0 \leq s < t$, $N_{t} - N_{s}$ is independent of ${N_{u}}_{u \leq s}$
Stationary increments: Distribution of $N_{t+h} - N_{t}$ does not depend on $t$, but only on $h$ for $h > 0$
Poisson distribution: For all $0 \leq s < t$, $N_{t} - N_{s} \sim Pois(\lambda (t-s))$
Poisson Distribution: $X\sim P(\lambda )$ \(P(X = k) = \frac{e^{-\lambda }\lambda^{k}}{k!}\)
SDEs for Option Pricing
Definition 46 (Economy). A probability space $\Omega , \mathcal{F} , (\mathcal{F}{t}: 0 \leq t \leq T), P$
Assume $\mathcal{F} = \mathcal{F}{t}$. We have 2 assets traded: a stock price $S_{t}$ and a bond price $B_{t}$ with the following:
Stock price: $dS_{t} = \mu S_{t}dt + \sigma S_{t}dW_{t}$
$\implies S_{t} = S_{0}\exp \left( {(\mu - \frac{1}{2}\sigma^{2})t + \sigma W_{t}}\right),\quad 0 \leq t \leq T$
Bond price: $dB_{t} = rB_{t}dt$
$\implies B_{t} = e^{rt}$
Assumptions:
No transaction costs: No costs to buy or sell assets
No dividends: Stock does not pay dividends
Shares are infinitely divisible: Can buy any fraction of a share
Short selling allowed: Can sell assets you do not own
No default risk
No funding costs: Cash can be borrowed or lent at the risk free rate $r$
Continuous time and continuous trading/hedging
Perfect market info, complete markets
Definition 47 (Contingent Claim). A contingent claim $Y$ for maturity $T$ is any square-integrable $(\mathbb{E}[Y^{2} ] < + \infty )$ and positive random variable in $\Omega , \mathcal{F}{t}, P$ which is in particular $\mathcal{F}{T}$-measurable. We limit ourselves to simple contingent claims, i.e. claims of the form $Y = f(S_{T})$, where $f$ is a measurable function of the risky asset at maturity.
Definition 48 (Trading Strategy). A trading strategy is a pair of processes $(\varphi^B, \varphi^S)$ on $\Omega , \mathcal{F} , (\mathcal{F}_{t}: 0 \leq t \leq T), P$ that are locally bounded and predictable. Representing the number of shares of the bond and stock respectively. We have the value of the portfolio at time $t$ given by: \(V_{t}(\varphi) = \varphi_{t}^{B}B_{t} + \varphi_{t}^{S}S_{t}\)
Definition 49 (Gain process). \(G_{t}(\phi ) = \int_0^t \phi_{s}^{S}dS_{s} + \int_0^t \phi_{s}^{B}dB_{s}\) representing the income from the trading strategy $\phi$ up to time $t$
Definition 50 (Self-financing). A strategy is self-financing if $V_{t}(\phi ) \geq 0$ for all $t \in [0,T]$ and
\[V_{t}(\phi ) = V_0(\phi ) + G_{t}(\phi )\]Or equivalently:
\[dV_{t}(\phi ) = \phi_{t}^{S}dS_{t} + \phi_{t}^{B}dB_{t} = dG_{t}(\phi )\]i.e only changes in value of portfolio come from changes in the value of the assets.
Definition 51 (Arbitrage). An arbitrage is a self-financing trading strategy $\phi$ such that: \(\phi_{0}^{B}B_{0} + \phi_{0}^{S}S_{0} = 0, \quad \mathbb{P}(V_{t}(\phi ) > 0) > 0\) i.e. a strategy that has no initial cost and has a positive probability of making a profit.
Definition 52 (Attainable contingent claims). A contingent claim $Y$ is attainable if there exists a self-financing trading strategy $\phi$ such that: \(V_{T}(\phi ) = Y\) Say that $\phi$ generates $Y$ $V_{t}(\phi )$ is the price at time $t$ for $Y$.
Definition 53 (European Call). A European call option is a contingent claim with payoff: \(Y = (S_{T} - K)^{+}\) where $K$ is the strike price.
Definition 54 (European Put). A European put option is a contingent claim with payoff: \(Y = (K - S_{T})^{+}\) where $K$ is the strike price.
Definition 55 (Risk-neutral measure). The risk-neutral measure is a measure $\mathbb{Q}$ on $(\Omega , \mathcal{F} )$ such that the discounted price process ${e^{-rt}S_{t}}_{t \geq 0}$ is a martingale under $\mathbb{Q}$. We have that: \(\frac{d\mathbb{Q}}{d\mathbb{P}} = \frac{e^{-rT}S_{0}}{\mathbb{E}[e^{-rT}S_{T}]}\)
Definition 56 (Black-Scholes-Merton Model). Assume value of simple claim at $t = T$ a function of $S_{t}$
\[V_{t} = V(t, S_{t}) = \phi_{t}^S S_{t} + \phi_{t}^B B_{t}\]Assume $V \in C^{1,2}([0,T] \times \mathbb{R}^+)$ i.e 2x differentiable w.r.t $S_{t}$ and 1x with $t$. Then by Ito’s formula:
\[\begin{aligned} dV_{t} &= \frac{\partial V}{\partial t}dt + \frac{\partial V}{\partial S}dS_{t} + \frac{1}{2}\frac{\partial^{2} V}{\partial S^{2}}dS_{t}^{2} \\ dS_{t} &= \mu S_{t}dt + \sigma S_{t}dW_{t}\\ dtdt &= 0, \quad dW_{t}dW_{t} = dt, \quad dtdW_{t} = 0 \end{aligned}\]We have that:
\[dV_{t} = \left( \frac{\partial V}{\partial t} + \mu S_{t}\frac{\partial V}{\partial S} + \frac{1}{2}\sigma^{2}S_{t}^{2}\frac{\partial^{2} V}{\partial S^{2}} \right)dt + \sigma S_{t}\frac{\partial V}{\partial S}dW_{t}\]Via the self-financing condition we get:
\[\text{For } 0 \leq t \leq T \quad \phi_{t}^S = \frac{\partial V}{\partial S}(t, S_{t}), \quad \phi_{t}^B = (V_{t} - \phi_{t}^S S_{t})/B_{t}\]Combining the below two equations we get:
\[\begin{aligned} dV(t,S_{t}) &= \phi_{t}^B dB_{t} + \phi_{t}^S dS_{t}\\ dV_{t} &= \left[V_{t}(t,S_{t}) - \frac{\partial V}{\partial S}(t, S_{t}) S_{t}\right]r dt + \frac{\partial V}{\partial S}(t, S_{t}) S_{t} (\mu dt + \sigma dW_{t}) \end{aligned}\]We now get the Black-Scholes PDE, for terminal condition $V(T,S_{T}) = f(S_{T}) = (S_{T}-K)^+$:
\[\frac{\partial V}{\partial t} + rS_{t}\frac{\partial V}{\partial S} + \frac{1}{2}\sigma^{2}S_{t}^{2}\frac{\partial^{2} V}{\partial S^{2}} = rV(t,S_{t})\]We have the following solution:
\[V_{BS}(t,S_{t},K,T,\sigma ,r) = S_{t}\Phi(d_{1}(t)) - Ke^{-r(T-t)}\Phi(d_{2}(t))\]where:
\[d_{1}(t) = \frac{\log \left( \frac{S_{t}}{K} \right) + (r + \frac{\sigma^{2}}{2})(T-t)}{\sigma \sqrt{T-t}},\quad d_{2}(t) = d_{1}(t) - \sigma \sqrt{T-t}\]Definition 57 (In-, At-, Out-of-the-money). We have the following definitions for options:
In-the-money: $S_{t} > K$
At-the-money: $S_{t} = K$
Out-of-the-money: $S_{t} < K$
Theorem 58 (Feynman-Kac Theorem). *Given a PDE of the form:
\[\frac{\partial V}{\partial t} + \mu(t,x)\frac{\partial V}{\partial x} + \frac{1}{2}\sigma^{2}(t,x)\frac{\partial^{2} V}{\partial x^{2}} - rV(t,x) = 0\]with terminal condition $V(T,x) = f(x)$, then the solution is given by:
\[V(t,x) = e^{-r(T-t)} \cdot \mathbb{E}^{Q} \left[ f(X_{T}) \mid X_{t} = x \right]\]where $X_{t}$ is the solution to the SDE:
\[dX_{t} = \mu(t,X_{t})dt + \sigma(t,X_{t})dW_{t}\]Where diffusion process $X_{t}$ has dynamics starting at $X_{t} = x$
\[dX_{s} = b(s,X_{s})ds + \sigma(s,X_{s})dW_{s}, s \geq t, X_{t} = x\]Take $b(x) = rx, \sigma(x) = \sigma x$ for Black-Scholes model. We get:
\[\begin{aligned} V_{BS}(0,S_0, K,T,\sigma^{2} ,r) &= e^{-rT} \mathbb{E}^{Q}_0[(S_{T} - K)^{+}]\\ &= S_{0}\Phi(d_{1}) - Ke^{-rT}\Phi(d_{2})\\ d_{1,2} &= \frac{\log \left( \frac{S_{0}}{K} \right) + (r \pm \frac{\sigma^{2}}{2})T}{\sigma \sqrt{T}} \end{aligned}\]Proposition 59 (Computing Call option delta). *Call option delta - the sensitivity of the option price to changes in the initial stock price: \(\phi^S(0) = \Delta_0 = \frac{\partial V_{BS} }{\partial S} = \Phi(d_{1})\)
Proposition 60 (Risk Netural Measure via Girsanov’s Theorem). Aim to move from
\[dS_{t} = \mu S_{t}dt + \sigma S_{t}dW_{t}\]to
\[dS_{t} = rS_{t}dt + \sigma S_{t}dW_{t}^{\mathbb{Q}}\]We have that:
\[\frac{d\mathbb{P}}{d\mathbb{Q}} = \exp \left\{ -\frac{1}{2} \left( \frac{\mu -r}{\sigma }\right)^{2} T - \frac{\mu - r}{\sigma }W_{T} \right\}\]Call $\frac{\mu -r}{\sigma }$ the market price of risk or Sharpe ratio.*
Definition 61 (Martingale Measure). A martingale measure is a measure $\mathbb{Q}$ on $(\Omega , \mathcal{F} )$ such that the discounted price process ${e^{-rt}S_{t}}_{t \geq 0}$ is a martingale under $\mathbb{Q}$. We have that:
\[\frac{d\mathbb{Q}}{d\mathbb{P}} = \frac{e^{-rT}S_{0}}{\mathbb{E}[e^{-rT}S_{T}]}\]which is equivalent to $S$ having drift rate $r$ under $\mathbb{Q}$
\[dS_{t} = S_{t}[rdt + \sigma dW_{t}^{\mathbb{Q}}],\ 0 \leq t \leq T\]Theorem 62 (1st Fundamental Theorem of Asset Pricing). A market is arbitrage-free if and only if there exists a risk-neutral measure $\mathbb{Q}$ equivalent to the real-world measure $\mathbb{P}$. If there exists a risk-neutral measure $\mathbb{Q}$ equivalent to the real-world measure $\mathbb{P}$, then there exists a unique attainable claim price that can be computed as the expectation of the claim under the risk-neutral measure.
Definition 63 (Complete market). A market is complete if every contingent claim is attainable.
Theorem 64 (2nd Fundamental Theorem of Asset Pricing). A market is complete if and only if there exists a unique risk-neutral measure $\mathbb{Q}$ equivalent to the real-world measure $\mathbb{P}$.
Definition 65 (Numeraire). A numeraire is a risk-free asset whose price is always 1. We can use the numeraire to price other assets.Canonically the numeraire is the bond price $B_{t}$ with dynamics: \(dB_{t} = rB_{t}dt\)
Definition 66 (Zero-Coupon Bonds). A zero-coupon bond is a bond that pays 1 at maturity. The price of a zero-coupon bond at time $t$ is given by: \(P(t,T) = e^{-r(T-t)}\) Can take $r$ as a Stochastic process, then we have: \(P(t,T) = \mathbb{E}^{Q}[e^{-\int_{t}^{T} r_{s}ds} \mid \mathcal{F}_{t}]\)
Definition 67 (Forward Contracts). A forward contract is an agreement to buy or sell an asset at a future date for a price agreed upon today. The price of a forward contract at time $t$ is given by:
\[F(t,T) = S_{t}e^{r(T-t)}\] \[V_{FWD}(S_0, K,r) = S_0 - Ke^{-rT}\]Definition 68 (Put-Call Parity). We have the following relationship between call and put options: \(\underbrace{(S_{T}-K)^+}_{\text{CallPrice} } - \underbrace{(K-S_{T})^{+}}_{\text{PutPrice} } = \underbrace{S_{T} - K}_{\text{ForwardPrice} }\) So we get that
\[V_{BS}^{PUT}(0,S_0,K,T,\sigma ,r) = Ke^{-rT}\Phi(-d_{2}) - S_0\Phi(-d_{1})\]And for the delta:
\[\Delta_{PUT} = - \Phi(-d_{1}) = \Phi(d_{1}) - 1\]Definition 69 (Dynamic Hedging). Dynamic hedging is the process of continuously adjusting the portfolio to maintain a delta-neutral position. We have that:
\[\Delta_{t} = \frac{\partial V_{t}}{\partial S_{t}}\]And so the number of shares of the stock/cash to hold is given by: \(\phi_{t}^S = \Delta_{t}, \quad \phi_{t}^B = (V_{t} - \Delta_{t}S_{t})/B_{t}\)
Theorem 70. Metatheorem/folklore: A market is complete if there are as many assets as independent sources of randomness. In reality markets are incomplete, as there are some risks that are covered by no direct assets, and there are more risks than assets.
This can be partly addressed by including a few derivatives themselves among the basic assets, but it is hard to keep the market complete
Example 71. For example, as we will see in the volatility smile part, in a stochastic volatility model like Heston for the stock price $S_t$ under the measure $\mathbb{Q}$,
\[\begin{aligned} dS_t &= rS_tdt + \underline{\sqrt{V_t}} S_tdW_t, \quad \text{so, } \quad dWdW^V = \rho dt \\ dV_t &= k(\theta - V_t)dt + \sigma\sqrt{V_t}dW^V_t, \quad V_0,\end{aligned}\]we have that now the volatility (see underlined) in the stock equation, namely $\sqrt{V_t}$, is a second stochastic differential equation driven by a second Brownian motion $W^V$. In Black Scholes the box would have a deterministic constant $\sigma$.
If we hedge only with the stock price $S_t$, delta hedging does not work because the risk associated with the randomness of the volatility is not covered by the stock, the stock is one asset and can only cover one risk, the risk of $W$, but not the risk of $W^V$.
Thus, if our only hedging risky asset is the stock $S$, in a Heston model the market is incomplete. To make the market complete we need to add another asset to the fundamental assets we start from.
For example, a specific call option $C$ with a given strike $K$ and maturity $T$ could be added to $\mathcal{B}_t$ and the stock, and the market would be complete again, because we would have two risky assets now, $S_t$ and $C_t$, to hedge two sources of risk, $W$ and $W^V$. A trading strategy would then have to be a triple now, $(\phi^B, \phi^S, \phi^C)$. In reality it’s not always possible to find a risky asset matching a given risk, this is particularly difficult or impossible for some credit risk, liquidity risk, operational risks, etc. Real market remains incomplete.
A further problem is that continuous rebalancing does not happen. Real hedging happens in discrete time and this will imply an hedging error with respect to the idealized case
Definition 72 (Sensitivities/Greeks). The Greeks are sensitivities of the option price to changes in the underlying asset price, time, volatility, and interest rate. We have the following Greeks:
Delta: (Change to Initial Price) $\Delta = \frac{\partial V}{\partial S}$
Gamma: (Change to Delta) $\Gamma = \frac{\partial^{2} V}{\partial S^{2}}$
Theta: (Time Decay) $\Theta = \frac{\partial V}{\partial t}$
Vega: (Change to Volatility) $\nu = \frac{\partial V}{\partial \sigma }$
Rho: (Change to Interest Rate) $\rho = \frac{\partial V}{\partial r}$
Lambda: (Leverage) $\lambda = \frac{\Delta S}{V}$
Speed: (Change to Gamma) $S = \frac{\partial^{3} V}{\partial S^{3}}$
Can use the above to rewrite Ito’s Formula (for a call option) as follows: \(dV(t,S_{t}) = \Theta dt + \Delta_{t} dS_{t} + \frac{1}{2}\sigma^{2} \Gamma_{t} dS_{t}^{2}\) If we have $\Theta < 0$ for a call option, the option loses value over time, and if $\Theta > 0$ the option gains value over time. We have $\Gamma$ to counteract the effect of $\Theta$ on the option price.
Intro to Volatility Smile {#intro-to-volatility-smile .unnumbered}
Definition 73 (Volatility Smile). The volatility smile is a pattern that results from the implied volatilities of options with the same underlying asset and expiration date but different strike prices. The smile is so named because it looks like a smile. The volatility smile is a graph of the implied volatility of option contracts at various strike prices.
Definition 74 (Implied Volatility). Implied volatility is the estimated volatility of a security’s price. In general, implied volatility increases when the market is bearish, when investors believe that the asset’s price will decline, and decreases when the market is bullish, when investors believe that the price will rise. It is a function of the options strike price.
Definition 75 (Volatility Surface). The volatility surface is a three-dimensional plot of the implied volatility of options at different strike prices and expiration dates. The volatility surface is used to show the relationship between volatility and moneyness.
Proposition 76 (Smile Modelling). Alternative SDE model for $dS$ can generate a non-flat smile:
Set $K$ to a starting value;
_Compute the model call option price
\[V_\text{Model}(K) = E_0^\mathbb{Q}\left[e^{-rT}(S_T - K)^+\right]\]with S modeled through an alternative dynamics (underlined)
\[\text{Model: } dS_t = rS_tdt + \underline{\sigma(t, S_t)}S_t dW_t, \quad S_0 = s_0\]_Invert Black Scholes formula for this strike, i.e. solve \(V_\text{Model}(K) = V\_\text{BS}(0, S_0, K, T, \nu(K), r).\)
in $\nu(K)$, thus obtaining the model implied volatility $\nu(K)$
Change K and restart from point 2.
At the end of this algorithm we have built the smile curve $K \mapsto \nu(K)$ for this model.
Definition 77 (Bachelier Model). The Bachelier model is a model for the dynamics of a stock price in which the volatility of the stock is constant. The model is used to price European options. The Bachelier model is a special case of the Black-Scholes model in which the volatility is zero. \(dS_{t} = \sigma dW_{t}^Q\) The price of a call option in the Bachelier model is given by: \(\mathbb{E}^{Q}[(S_{T} - K)^{+}] = (S_{0} - K)N(d)\) \(V_{BaM}(0,S_0,K,T,\sigma ,r) = (s_0 - K) \Phi (d) + \sigma \sqrt{T} p_{N} (d), \quad d = \frac{s_0 - K}{\sigma \sqrt{T}}\) We get the smile curve by inverting the Black-Scholes formula for the Bachelier model. \(V_{BS}(0,S_0,K,T,\nu(K) ,r) \rvert_{r=0} = V_{BaM}(0,S_0,K,T,\sigma)\)
Definition 78 (Displaced Diffusion Model). Here we define:
\[dS_{t} = rS_{t} dt + \sigma (S_{t}- \alpha e^{rt} ) dW_{t}\]See that the drift is now $rS_{t}$ and so arbitrage free. The price of a call option in the Displaced Diffusion model is given by:
\[V_{DDM}(0,S_0,K,T,\sigma ,r) = (S_0 - \alpha ) \Phi (d_1(0)) - K e^{-rT} \Phi (d_2(0))\] \[d_1(0) = \frac{\log \left( \frac{S_0 - \alpha }{K - \alpha e^{rt} } \right) + (r + \frac{\sigma^{2} }{2})T}{\sigma \sqrt{T}}, \quad d_2(0) = d_1(0) - \sigma \sqrt{T}\]Generating the smile curve by inverting the Black-Scholes formula for the Displaced Diffusion model.
\[V_{BS}(0,S_0,K,T,\nu(K) ,r) = V_{DDM}(0,S_0,K,T,\sigma, \alpha ,r)\]Definition 79 (CEV Model). Constant Elasticity of Variance (CEV) model is a model for the dynamics of a stock price in which the volatility of the stock is a power function of the stock price.
\[dS_{t} = r S_{t} dt + \nu S_{t}^{\gamma } dW_{t}, \quad S_0 = s_0\]where $\gamma$ is the elasticity of variance, we take $\gamma$ between 0 and 1 . For $\gamma = \frac{1}{2}$ we call it the "Feller Square root process". For $\gamma <1$, need to say what happens at $S = 0$, usually taken as absorbing boundary.
Definition 80 (Mixture Diffusion Dynamics). FILL THIS LATER
Definition 81 (The Shifted Mixture Dynamics model). FILL THIS LATER
Definition 82 (Stochastic Volatility Models). The models above are all called local volatility models. In these models the volatility $\sigma(t,S_{t})$ in the SDE
\[dS_{t} = rS_{t}dt + \sigma(t,S_{t})S_{t}dW_{t}, s_0\]is a deterministic function of time and the stock price only. In stochastic volatility models, the volatility is itself a stochastic process.
FILL THE REST OF THIS LATER TOO pg 280 in original notes.
Risk Measures
Proposition 83 (Distribution of log-returns). From Black-Scholes under measure $P$ we have for stock $S{t}$ \(S_{t} = S_0 \exp \left\{ \left( \mu - \frac{1}{2}\sigma^{2}\right)t + \sigma W_{t} \right\} \quad 0 \leq t \leq T\) Taking logs we get, with $\delta = t_{i+1} - t_{i}$ \(\log \frac{S_{t_{i+1}} }{S_{t_{i}}} = \left( \mu - \frac{1}{2}\sigma^{2}\right)\delta + \sigma (W_{t_{i+1}} - W_{t_{i}}) \sim \mathcal{N} \left( \left( \mu - \frac{1}{2}\sigma^{2}\right)\delta , \sigma^{2}\delta \right)\) Gaussian distribution! can test this with QQ plots, or sample skewness and kurtosis, both should be 0.
\[\text{Skewness} = \frac{\mathbb{E}[(X - \mathbb{E}[X])^{3}]}{\sigma^{3}}, \quad \text{Kurtosis} = \frac{\mathbb{E}[(X - \mathbb{E}[X])^{4}]}{\sigma^{4}}\]Definition 84 (VaR - Value at Risk). Defined simply as the loss level that will not be exceeded with a certain confidence level over a certain period of time
Value at Risk (VaR) is a measure of the risk of loss for investments. It estimates how much a set of investments might lose (with a given probability), given normal market conditions, in a set time period such as a day. VaR is typically used by firms and regulators in the financial industry to gauge the amount of assets needed to cover possible losses. \(\text{VaR}_{\alpha } = -\inf \{x \in \mathbb{R} : P(X \leq x) \geq \alpha \}\) where $\alpha$ is the confidence level, and $X$ is the loss distribution.
Also define $L_{H}$
\[L_{H} = \text{Portfolio}_0 - \text{Portfolio}_{H}\]and take $\Pi(t,T)$ the sum of all future cash flows from the portfolio in $[t,T]$ discounted back at $t$, for our portfolio.
This gives us the price of the portfolio at time $t$, for $T$ final maturity.
This gives us $VaR_{H,\alpha }$, for horizon $H$ and confidence level $\alpha$, satisfying:
\[\mathbb{P} \left( L_{H} < VaR_{H,\alpha } \right) = \alpha\]Or equiv.
\[\mathbb{P} \left( \mathbb{E}_0^{\mathbb{Q}} [\Pi (0,T)] - \mathbb{E}_H^{\mathbb{Q}} [\Pi (H,T)] < VaR_{H,\alpha } \right) = \alpha\]Proposition 85 (Drawbacks to VaR).
*Does not take into account the tail structure beyond the percentile. Refer to figure below:*
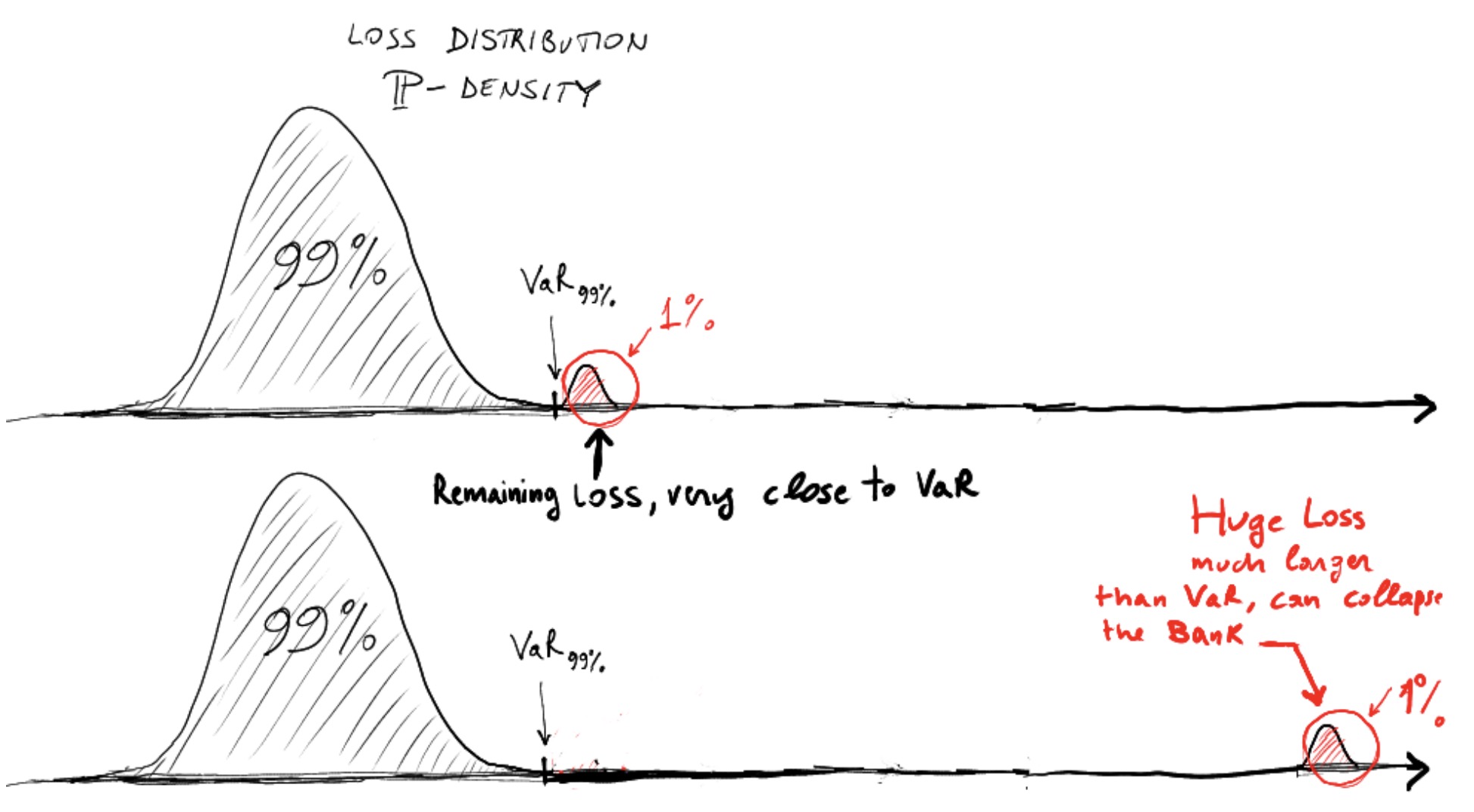
From the picture above we see that we may have two situations where the VaR is the same but where the risks in the tail are dramatically different. In the first case, the VaR singles out a 99% percentile, after which a slightly larger loss follows with 1% probability mass. The bank may be happy to know the 99% percentile in this case and to base its risk decision on that. In the second case, the VaR singles out the same 99% percentile, after which an enormously much larger loss concentration follows with probability 1%. For example, this is now so large to easily collapse the bank. Would the bank be happy to ignore this potential huge and devastating loss, even if it has a small 1% probability?
*VaR is not subadditive, i.e. the VaR of a portfolio is not the sum of the VaR of the individual assets. This is because VaR is a quantile, and quantiles are not additive.*
Definition 86 (ES - Expected Shortfall). Used as a solution to (2) and a partial solution to (1) above.
Expected Shortfall (ES) is a risk measure that quantifies the average loss of the tail of the loss distribution. It is an alternative to Value at Risk that is more sensitive to the shape of the tail of the loss distribution. ES is also known as Conditional Value at Risk (CVaR) or Expected Tail Loss (ETL).
Proposition 87 (Drawbacks to ES).
Does not fully solve the problem of (1) above, as it still only considers the average loss in the tail, not the full tail structure.
liquidity risk - common with VaR and ES, as they do not take into account the liquidity of the assets in the portfolio. Namely:
\[\begin{aligned} VaR(k \cdot \text{Portfolio}) &\neq k \cdot VaR(\text{Portfolio})\\ ES(k \cdot \text{Portfolio}) &\neq k \cdot ES(\text{Portfolio}) \end{aligned}\]Selling a million shares of a stock will not be as easy as selling one share, and so the risk of the portfolio is not linear with the size of the portfolio.
Numerical Solutions of SDEs
Definition 88 (Euler Scheme). The Euler scheme is a simple numerical method to solve SDEs. It is a first-order method, and is not very accurate. Let time step be $\Delta t = t_{i+1} - t_{i} = \delta \forall i$ and write $\Delta W_{t_{i}} = W_{t_{i+1}} - W_{t_{i}}, \Delta X_{t_{i}} = X_{t_{i+1}} - X_{t_{i}}$. We have: \(\Delta X_{t_{i}} = \mu (t_{i}, X_{t_{i}})\Delta t_{i} + \sigma (t_{i}, X_{t_{i}})\Delta W_{t_{i}},\quad X_0 = Z\) and writing \(\Delta W_{t_{i}} = W_{t_{i+1}} - W_{t_{i}} \sim \sqrt{\delta} \mathcal{N}_{i}(0,1)\) where $\mathcal{N}_{i}(0,1)$ is a standard normal and all normals are independent. We get the Euler scheme: \(X_{t_{i+1}} = X_{t_{i}} + \mu (t_{i}, X_{t_{i}})\delta + \sigma (t_{i}, X_{t_{i}})\sqrt{\delta} \mathcal{N}_{i}(0,1), \quad X_0 = Z\)
Proposition 89 (Convergence of Euler Scheme). _The Euler scheme converges to under sufficient conditions for existence and uniqueness of the global solution of our SDE. These are Lipschitz continuity and linear growth conditions on $\mu$ and $\sigma$. We have an order of convergence of $\frac{1}{2}$. We have that there exists a positive real number $\delta_0$ such that \(E\{ \left\vert X_{T}^{\Delta t} - X*{T} \right\vert \} \leq C(T) (\Delta t)^{\frac{1}{2}} \quad \forall \Delta t \leq \delta_0\) Where $C(T)>0$ a constant*