Algebra 3 - Concise Notes
MATH60035
PDFs
Problem Sheets
Table of contents
Rings
Basic Definitions and Examples
Definition 1. A monoid $(M, \cdot )$ a set $M$ and binary op $\cdot \colon M \times M \to M$, with $1_{M} \in M$ s.t
$m \cdot 1_M = m = 1_M \cdot m \forall m \in M$
Operation $\cdot$ is associative, $x \cdot (y \cdot z) = (x \cdot y) \cdot z$
Definition 2. A *ring a set $(R, + : R \times R \to R, \cdot : R\times R \to R)$ with elements $0_R,1_R \in R$ s.t*
$(R,+)$ an abelian group with identity $0_R$
$(R,\cdot )$ a monoid with identity $1_R$
Distributivity: $a(b+c) = ab + ac, (b+c)a = ba + ca$
*Note: write additive inverse as $-r$*
Definition 3. Say $R$ a ring *commutative if $a \cdot b = b \cdot a, \forall a,b \in R$*
Definition 4. For $S \subset R$ , $R$ a ring. Say $S$ a *subring of $R$ if*
$0_R, 1_R \in S$
$+, \cdot$ make $S$ into a ring with identities $0_R,1_{R}$
We write $S \leq R$
Proposition 5. $R$ a ring, $1_R = 0_R \iff R = {0}$ the trivial ring
Definition 6. $u \in R$ a unit, if $\exists v \in R$ s.t $u \cdot v = v \cdot u = 1_R$
\[R^{\times } \subseteq R, \text{ the set of units in } R\]Definition 7. A division ring a non-trivial ring, s.t every $u \neq 0_R \in R$ a unit.
\[R^{\times } = R \backslash \{0\}\]A Field a commutative division ring*
Proposition 8. Subset $R^{\times } \subset R$ a group under multiplication.
Constructions of rings
Example 9. $R,S$ rings $\implies R \times S$ the product ring a ring via \((r,s) + (r^\prime ,s^\prime ) = (r + r^\prime ,s + s^\prime ) \quad (r,s)\cdot (r^\prime ,s^\prime ) = (r\cdot r^\prime ,s \cdot s^\prime )\)
Example 10. $R$ a ring, the polynomial ring $R[X]$ a ring \(R[X] = \{f = a_0 + a_1 X + \ldots a_n X^n \mid a_i \in R \}\)
So for $f = \sum_{i=1}^{n} a_i X^i$, $g = \sum_{i=1}^{k} b_i X^i$, we have ring ops
\[f + g := \sum_{r=0}^{\mathop{\max} \{n,m\}} (a_{i} + b_{i}) X^i\] \[f \cdot g := \sum_{i=0}^{n + k} \left( \sum_{j=0}^{i} a_{j}b_{i-j} \right) X^i\]Note: call maximal $n$ s.t $a_n \neq 0R$ the $deg(f)$
For $f$ of degree $n \geq 0$, if $a{n}=1$ say $f$ is monic.
Notation: Write $R[X,Y]$ for $(R[X])[Y]$ polynomial ring in 2 variables, and in general $R[X_1, \ldots , X_n] = (\ldots ((R[X_1])[X_2]\ldots )[X_n] )$
Example 11. *Laurent polynomials on $R$ the set $R[X,X^{-1} ]$
\[R[X,X^{-1} ] = \left\{f = \sum_{i\in \mathbb{Z}} a_{i}X^i \mid \text{ only finitely many } a_i \neq 0 \right\}\]Operations defined similarly to $R[X]$
We have here the set of monomials ${X^i: i \in \mathbb{Z}}$ form a group under multiplication.*
Example 12. $G$ a group, $R$ a ring. Define the *Group Ring $R[G]$:
\[R[G] := \left\{\sum_{g\in G} a_{g}g \mid a_{g} \in R, |\{g\in G: a_{g}\neq 0\}| < \infty \right\}\]With addition and multiplication as follows
\[\left( \sum_{g\in G} a_{g}g \right) + \left( \sum_{g\in G} b_{g}g \right) = \sum_{g\in G} (a_{g} +_{R} b_{g} )g\] \[\left( \sum_{g\in G} a_{g}g \right) \cdot \left( \sum_{g\in G} b_{g} g \right) = \sum_{g\in G} \left( \sum_{h \in G} a_{h} \cdot_{R} b_{h^{-1}g} \right) g\]We have that $R[X,X^{-1} ] \cong R[C_\infty], C_\infty = (\mathbb{Z}, + )$
If $R$ commutative ring, then $R[G]$ commutative $\iff G$ abelian.*
Example 13.
*\(M_{n}(R) = \text{ set of } n\times n \text{ matrices},\ R \text{ a ring}\)
A ring over the usual addition and multiplication*
Example 14. *Abelian group $A$
\[\mathop{End}(A) = \{f:A \to A\mid f \text{ a group homomorphism} \}\]A ring with ops
\[(f +_{\mathop{End}(A)} g)(x) := f(x) +_{A} g(x) \quad (f \cdot_{\mathop{End}(A)} g)(x) := (f \circ g)(x)\]Group of units of $\mathop{End}(A)$ is the automorphism group of $A$ denoted $\mathop{Aut}(A)$*
Homomorphisms, ideals and quotients
Definition 15. $R,S$ rings. $\varphi : R \to S$ a ring homomorphism if
$\varphi (r_1 + r_2) = \varphi (r_1) + \varphi (r_2)$
$\varphi (0_R) = 0_S$
$\varphi (r_1 \cdot r_2) = \varphi (r_1) + \varphi (r_2)$
$\varphi (1_R) = 1_S$
Definition 16. An isomorphism, A bijective homomorphism $\varphi$
Definition 17. Kernel of homomorphism $\varphi : R \to S$
\[\mathop{ker}(\varphi ) = \{r \in R: \varphi (r) = 0_S\}\]Definition 18. Image of homomorphism $\varphi : R \to S$
\[\mathop{im}(\varphi ) = \{s \in S: s = \varphi (r), \text{ for some } r \in R \}\]Lemma 19. Homomorphism $\varphi : R \to S$ injective $\iff \mathop{ker}\varphi = {0_R}$
Definition 20. A ideal $I \subset R$ an abelian subgroup s.t
\[\forall i \in I, r \in R \begin{cases} ri \in I, &\text{ left ideal } \\ ir \in I, &\text{ right ideal } \end{cases}\]This the strong closure property.
A two-sided or bi-ideal both a left and right ideal.
Lemma 21. $\varphi : R\to S$ a homomorphism, then $\mathop{ker}(\varphi ) \subset R$ a two-sided ideal
Definition 22. *Proper ideal, an ideal $I \neq R$
For every proper ideal $I$, we have $1 \notin I$ $\implies$ not a subring.
Even more generally, proper ideals do not contain any unit.
Definition 23. *For element $a \in R$, write the ideal generated by $a$ as,
\[(a) = Ra = \{r \cdot a \mid r \in R\} \subset R\]The ideal generated by $a_1, \ldots a_n$
\[\begin{pmatrix} a_1, \ldots ,a_n \end{pmatrix} = \{r_1 a_1 + \ldots r_k a_k \mid r_i \in R\}\]Definition 24. *$A \subset R$ define ideal generated by $A$ as
\[(A) = R \cdot A = \left\{ \\sum_{a \in A} r_{a} \cdot a \mid r_{a}\in R, \text{ only finitely many non-zero} \right\}\]Definition 25. Say ideal $I$ principal if $I = (a)$ for some $a \in R$
Definition 26. Let $I \subset R$ a two-sided ideal
Quotient ring $R/I = {r + I \mid r \in R}$ a ring with $0_R + I, 1_R + I$
Proposition 27. Quotient ring a ring, and function
\[\varphi \colon R \to R/I, r \mapsto r + I\]a ring homomorphism.
Proposition 28. (Euclidean algorithm for polynomials)
Let $F$ a field, and $f,g \in F[X] \implies \exists r,q \in F[X]$ s.t
with $\mathop{deg } r < \mathop{deg } g$
Theorem 29. *(First isomorphism theorem)
Let $\varphi :R \to S$ a ring homomorphism, $\mathop{ker}(\varphi) \subseteq R$ a 2-sided ideal and
Theorem 30. (Second isomorphism theorem)
$R \leq S$ be subrings, $J \subseteq S$ a 2-sided ideal. Then
(i) $R+ J = {r + j: r\in R, j \in J} \leq S$ a subring
(ii) $J \subseteq R + J$ and $J \cap R \subseteq R$ are both 2-sided ideal
(iii) $\frac{R+J}{J} = {r + J: r\in R} \leq \frac{S}{J} \leq \frac{S}{J}$ a subring, and $\frac{R}{R \cap J} \cong \frac{R+J}{J}$
Theorem 31. (Third isomorphism theorem)
Let $R$ a ring, $I,J \subseteq R$ 2-sided ideals s.t $I \subseteq J$ Then $J/I \subseteq R/I$ a 2-sided ideal and
Integral Domains
Integral domains, maximal and prime ideals
Definition 32. $R$ a commutative ring. Element $x \in R$ a *zero divisor if $x \neq 0, \exists y \neq 0 \text{ s.t } x \cdot y = 0 \in R$*
Definition 33. Integral domain (ID) a non-trivial commutative ring without zero divisors
\[\text{a ring where if } ab = 0 \implies a = 0 \text{ or } b = 0\]Lemma 34. $R$ a finite ring, and integral domain $\implies R$ a field.
Lemma 35. $R$ an integral domain. Then $R[X]$ an integral domain
Lemma 36. A non-trivial commutative ring $R$ a field $\iff$ its only ideals are ${0}$ and $R$
Definition 37. An ideal $I$ of ring $R$ maximal if $I \neq R$ and for any ideal $J$ s.t $I \leq J \leq R$ either $J = I$ or $J = R$
Lemma 38. $R$ a commutative ring. $I \subseteq R$ maximal $\iff$ $R/I$ is a field
Definition 39. Ideal $I \subseteq R$ is prime if $I \neq R$ and if $a,b \in R$ s.t $a \cdot b \in I \implies a \in I$ or $b \in I$
Lemma 40. $R$ a commutative ring. $I \subseteq R$ ideal, prime $\iff$ $R/I$ is an integral domain
Corollary 41. $R$ commutative ring. Then every maximal ideal is a prime ideal.
Definition 42. $R$ a ring. $\iota : \mathbb{Z} \to R$ the unique such map. The *characteristic of $R$ the unique non-negative $n$ s.t $\mathop{ker}(\iota ) = n \mathbb{Z}$*
Lemma 43. $R$ an integral domain. $\mathop{char}(R) = 0$ or $p$ a prime number.
Factorisation in Integral domains
Definition 44. $R$ a ring. Say for $a,b \in R$ $a$ divides $b$, $a \mid b$ if $\exists c \in R$ s.t $b = ac$. Equivalently $(b) \subseteq (a)$
Definition 45. $R$ a ring, say $a,b \in R$ associates if $a = bc$ for some $c \in R^{\times }$ a unit. Equivalently $(a) = (b)$ or $a \mid b$ and ${b \mid a}$
Definition 46. $R$ a ring. $a \in R$ irreducible if $a \neq 0$, and $a \notin R^{\times }$ and if $a = xy \implies x \in R^{\times}$ or $y \in R^{\times }$
Definition 47. $R$ a ring. $a \in R$ prime if $a \neq 0$ and $a \notin R^{\times }$ and if $a | xy \implies a|x$ or $a |y$
Lemma 48. A principal ideal $(r)$ prime ideal in $R$ $\iff r = 0$ or $r$ prime
Lemma 49. If $r \in R$ prime, then $r$ irreducible
Definition 50. (Euclidean domain)
An integral domain $R$ a Euclidean Domain (ED) if $\exists$ Euclidean function $\phi : R\backslash {0} \to \mathbb{Z}_{\geq 0}$ s.t
$\phi (a \cdot b) \geq \phi (b), \forall a,b \neq 0$
If $a,b \in R, b \neq 0 \implies \exists q,r \in R$ s.t
\[a = b \cdot q + r\]With either $r = 0$ or $\phi (r) < \phi (b)$*
Definition 51. *(Principal ideal domain)
A ring $R$, an integral domain, is a principal ideal domain (PID) if every ideal is a principal ideal.
Proposition 52. Let $R$ a Euclidean domain. Then $R$ a principal ideal domain
Definition 53. (Unique factorisation domain)
An integral domain a unique factorisation domain (UFD) if
Every non-unit written as product of irreducibles
If $p_1 \ldots p_n = q_1 \ldots q_m$ with $p_i, q_j$ irreducibles, then $n = m$ and they can be reordered s.t $p_i$ is an associate of $q_i$
Theorem 54. (PID $\implies$ UFD)
If $R$ a principal ideal domain, then $R$ a unique factorisation domain.
Lemma 55. $R$ a PID, then a principal ideal $(r)$ maximal $\iff$ $r$ irreducible or, if $R$ a field, $r = 0$
Proposition 56. $R$ a PID, if $r \in R$ irreducible then $r$ prime.
Corollary 57. $R$ a PID, Then every non-zero prime ideal is maximal
Definition 58. *(ACC - Ascending Chain Condition)
A commutative ring satisfies the ACC, if
Then $\exists N \in \mathbb{N}$ s.t $I_n = I_n + 1$ for some $n \geq N$*
Definition 59. (Noetherian Ring)
A commutative ring satisfying the ACC is Noetherian.
Proposition 60. $R$ a PID $\implies$ $R$ Noetherian
Definition 61. (Greatest Common Divisor, gcd)
$R$ a ring, $d$ a (gcd) of $a_1,a_2, \ldots , a_n$ if $d | a_{i}, \forall i$ and if any other $d^\prime$ satisfies $d^\prime | a_{i}, \forall i$ then $d^\prime | d$
Lemma 62. $R$ a UFD $\implies$ (gcd) exists and is unique up to associates.
i.e if $d, d^\prime$ are gcds of $a_1, a_2 , \ldots a_n$ then $d, d^\prime$ are associates.
The above lemmas and theorems yield the following chain of implications
\[\underbrace{(\mathbb{Z})}_{\text{isomorphic to } \mathbb{Z} } \implies \text{ED} \implies \text{PID} \implies \text{UFD} \implies \text{ID} \implies \text{Commutative Ring} \implies \text{Ring}\] \[(\mathbb{Z}) \underbrace{\not\Leftarrow}_{\mathbb{Q}, \mathbb{Z}[i]} \text{ED} \underbrace{\not\Leftarrow}_{\mathbb{Z}[\frac{1 + \sqrt{-19} }{2}]} \text{PID} \underbrace{\not\Leftarrow}_{\mathbb{Z}[X]} \text{UFD} \underbrace{\not\Leftarrow}_{\mathbb{Z}[\sqrt{-5} ]} \text{ID} \underbrace{\not\Leftarrow}_{\mathbb{Z}/6\mathbb{Z}} \text{Commutative Ring} \underbrace{\not\Leftarrow}_{M_2(\mathbb{Z})} \text{Ring}\]Localisation
Definition 63. *$R$ an ID, $S \subseteq (R, \cdot )$ a multiplicative submonoid. $0 \notin S$. Localisation is set of equivalence classes
\[S^{-1} R = \left\{(r,s) \mid r \in R, s \in S, (r,s) \sim (r^\prime ,s^\prime) \text{ if } rs^\prime = r^\prime s)\right\}\]Pair $(r,s)$ denoted $\frac{r}{s}$ - this is a ring with ops.
\[(r,s) \cdot (r^\prime , s^\prime ) := (r r^\prime ,s s^\prime),\quad (r,s) + (r^\prime ,s^\prime ) = (r s^\prime + r^\prime s,s s^\prime )\]Definition 64. $R = \mathbb{Z}, S = R \backslash {0}$, Then the rational numbers $\mathbb{Q}$ defined as $S^{-1} R$
Proposition 65. $R$ an ID, $S$ a multiplicative submonoid s.t $0 \notin S$ Then the map $\iota :R \to S^{-1} R$ is injective
Definition 66. *$R$ a commutative ring, $S \subseteq R$ a submonoid.
Localisation
Note we have $t$ in this definition when we move away from $R$ being an integral domain.*
Definition 67. If $R$ an integral domain $S = R\backslash{0}$, we have $S^{-1} R$ field. Define the field of fractions of $R$, $\mathop{Frac}(R) := S^{-1} R$
Proposition 68. (Universal property of localisation)
If $A$ a commutative ring, and $\varphi :R \to A$ a ring homomorphism, s.t $\varphi (S) \subset A^{\times }$ then, $\varphi$ factors through the homomorphism $\iota :R \to S^{-1} R$ i.e $\exists ! \widetilde{\varphi} :S^{-1} R \to A$ s.t $\varphi = \iota \circ \widetilde{\varphi}$
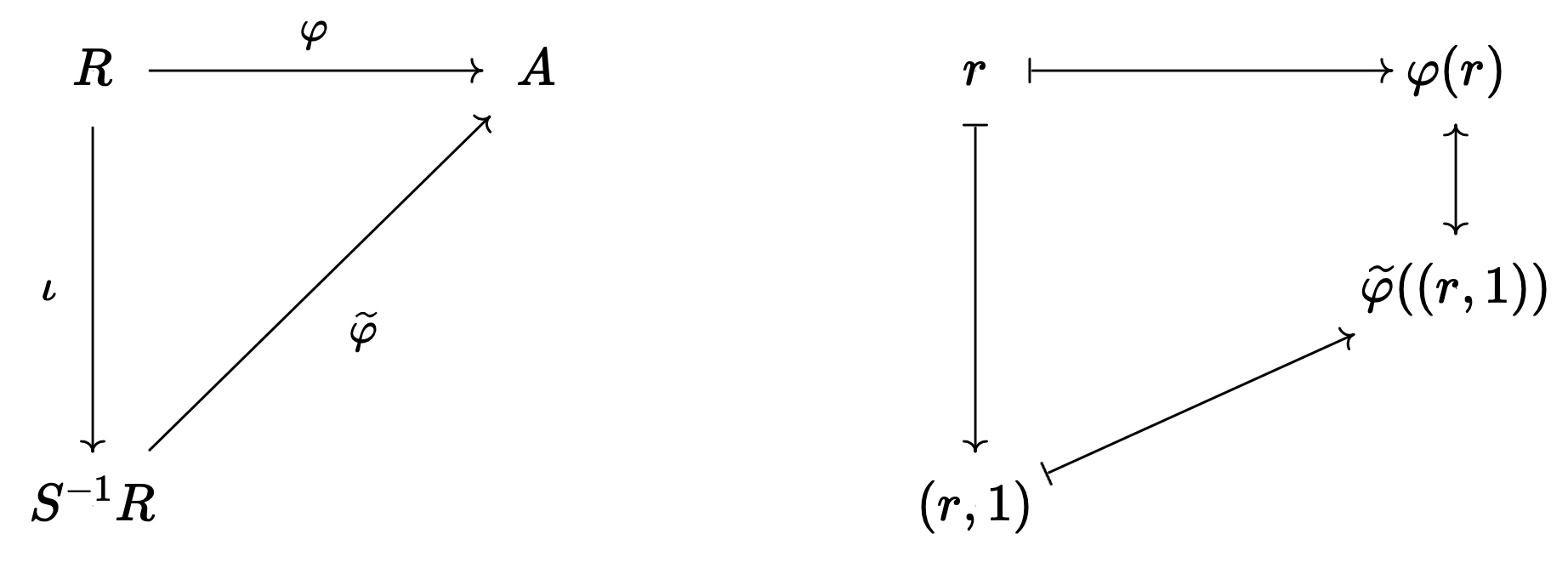
Definition 69. $R$ a commutative ring, $S \subseteq R$ a multiplicative submonoid.
Localisation, $S^{-1} R$ the unique ring $R^\prime$ s.t $\exists \iota R \to R’$ s.t
$\iota (S) \subseteq (R^\prime )^{\times}$
For all commutative rings $A$ and maps $\varphi :R \to A$ with $\varphi (S) \subseteq A^{\times }$, $\exists !\ \widetilde{\varphi} :R^\prime \to A$ s.t $\varphi = \widetilde{\varphi} \circ \iota$
Corollary 70. $R$ an ID, $F$ a field, $\varphi :R \to F$ an injective ring homomorphism. Then $\varphi$ factors through the map from $R$ to $\mathop{Frac}(R)$: $\varphi = \iota \circ \widetilde{\varphi}$ for $\iota :R \to \mathop{Frac}(R)$ with $\widetilde{\varphi}$ injective
Corollary 71. $F$ a field, $\mathop{charm}(F) = 0$. $F$ has subfield isomorphic to $\mathbb{Q}$
If $\mathop{char}(F) = p$ contains subfield isomorphic to $\mathbb{F}_{p}$
Lemma 72. $F$ a field, $F \leq R$ a subring $\implies R$ a vector space over $F$
Corollary 73. Every field a vector space over $\mathbb{F}_{p}$ or $\mathbb{Q}$
Example 74. $R$ a commutative ring. $I \subset R$ a prime ideal, $S = R \backslash I$ also a multiplicative submonoid.
Denote $S^{-1} R$ as $R_{I}$
Proposition 75. $R$ a commutative ring, $I \subseteq R$ a prime ideal. Then $R_{I}$ has a unique maximal ideal given by $\overline{I} = {(r,s) : r \in I, s\in R\backslash I}$
Definition 76. A local ring a ring which has a unique maximal ideal
Definition 77. Set $S^{-1} I := {\frac{i}{s}\mid s \in S, i \in I}$ an ideal in $S^{-1} R$ call this the image of $I$ under the localisation
Proposition 78. Every ideal $I \subseteq S^{-1} R$ of form $S^{-1} J$ for some $J \subseteq R$ an ideal.
Polynomial Rings
Factorisation in polynomial rings and Gauss’ Lemma
Definition 79. *$R$ a UFD, $f = a_0 + a_{1} X + \ldots a_n X^n \in R[X]$. The content is
\[c(f) = gcd \begin{pmatrix} a_0, \ldots ,a_n \end{pmatrix} \in R\]Equivalently define content as the ideal $(gcd \begin{pmatrix} a_0, \ldots ,a_n \end{pmatrix})$*
Definition 80. A polynomial is primitive if $c(f) \in R^{\times }$, the $a_{i}$ are coprime
Or as an ideal we have $c(f) = R[X]$
Lemma 81. $R$ a UFD, if $f\in R[X]$ then $f = c(f) \cdot f_1$ for some $f_1 \in R[X]$ primitive
Lemma 82. Let $R$ A UFD. If $f,g \in R[X]$ primitive then $fg$ primitive.
Corollary 83. Let $R$ a UFD. $f,g \in R[X]$ we have $c(fg)$ is an associate of $c(f)c(g)$
Lemma 84. (Gauss’ Lemma)
Let $R$ a UFD and $f \in R[X]$ a primitive polynomial. Then $f$ irreducible in $R[X] \iff f$ irreducible $F[X]$ where $F= \mathop{Frac}(R)$
Theorem 85. (Polynomial rings over UFDs)
If $R$ a UFD, then $R[X]$a UFD.
Further if $R$ a UFD then $R[X_1, \ldots , X_n]$ a UFD
Proposition 86. (Eisenstein’s Criterion)
$R$ a UFD, We let \(f = a_0 + a_{1}X + \ldots + a_{n}X^n \ \in R[X]\) be primitive with $a_{n} \neq 0$. Let $p \in R$ irreducible s.t
$p \nmid a_{n}$
$p \mid a_{i}\ \forall 0 \leq i \leq n$
$p^{2} \nmid a_0$
Then $f$ irreducible in $R[X]$ and hence in $\mathop{Frac}(R)[X]$
Algebraic Integers
Definition 87. *$\alpha \in \mathbb{C}$ an algebraic integer if \(\exists \text{ monic } f \in \mathbb{Z}[X] \text{ s.t } f(\alpha) = 0\)
Definition 88. *$\alpha$ algebraic integer, write $\mathbb{Z}[\alpha] \leq \mathbb{C}$ for smallest subring containing $\alpha$
Construct $\mathbb{Z}[\alpha]$ by taking it as image of $\phi : \mathbb{Z}[X] \to \mathbb{C}$ given by $g \mapsto g(\alpha )$ with $\phi$ inducing an isomorphism \(\mathbb{Z}[X] / I \cong \mathbb{Z}[\alpha],\quad I = \mathop{ker}\phi\)
Proposition 89. $\alpha \in \mathbb{C}$ an algebraic integer and let $\phi : \mathbb{Z}[X] \to \mathbb{C}$ the ring homomorphism given by $f \mapsto f(\alpha )$ Then ideal \(I = \mathop{ker}(\phi )\) is principal with $I = (f_\alpha )$ for some irreducible monic $f_\alpha$
Definition 90. Let $\alpha \in \mathbb{C}$ an algebraic integer. Then minimal polynomial a polynomial $f_\alpha$ is the irreducible monice s.t $I = \mathop{ker}(\phi) = (f_\alpha )$
Lemma 91. Let $\alpha \in \mathbb{Q}$ be an algebraic integer. Then $\alpha \in \mathbb{Z}$
Noetherian rings and Hilbert’s basis theorem
Definition 92. A commutative ring Noetherian if it satisfies the ACC (see Def. 2.46)
Definition 93. Ideal $I$ finitely generated if can be written as $I= \begin{pmatrix} r_1, \ldots ,r_n \end{pmatrix}$ for some $r_1, \ldots ,r_n \in R$
Proposition 94. *A commutative ring is Noetherian $\iff$ every ideal is finitely generated.
*Note: PID trivially satisfy this.**
Proposition 95. $R$ Noetherian, and $I \subseteq R$ an ideal $\implies R / I$ Noetherian.
Theorem 96. (Hilbert’s basis theorem)
$R$ a Noetherian ring, $\implies R[X]$ also Noetherian.
Modules
Basic definitions and examples
Definition 97. $R$ a ring. A left R-module $(\underbrace{M}_{\text{set} }, \underbrace{+: M \times M \to M}_{addition}, \underbrace{\cdot : R \times M \to M}_{mult})$ with $0_{M} \in M$ s.t
- $(M,+)$ an abelian group with identity $0_{M}$
And we have $\cdot$ satisfying the following
(i) $(r_1 + r_2) \cdot m = (r_1 \cdot m) + (r_2 \cdot m)$
(ii) $r \cdot (m_1 + m_2) = (r \cdot m_1) + (r \cdot m_2)$
(iii) $r_1 \cdot (r_2 \cdot m) = (r_1 \cdot r_2) \cdot m$
(iv) $1_{R}\cdot m = m$
Right-module is the same but we have now $(\cdot : M \times R \to M)$ with (iii) now as $(m \cdot r_1) \cdot r_2 = m \cdot (r_1 \cdot r_2)$
Definition 98. $R$ a ring.
$R$-module an abelian group M, equipped with ring homomorphism
*\(\varphi : R \longrightarrow \underbrace{\mathop{End}(M)}_{\{f:M \to M \mid f \text{ a group hom.} \}}\)
Such that
\[\begin{aligned} \cdot \colon R\times M & \longrightarrow M \\ (r,m) & \longmapsto \varphi(r)(m) \end{aligned}\]Constructions of modules
Definition 99. *Let $M_1, M_2, \ldots , M_k$ be $R$- modules. Direct sum is also an $R$-module
\[M_1 \oplus M_2 \oplus \ldots \oplus M_{k}\]Which is the set $M_1 \times \ldots \times M_{k}$ with addition given by
\[\begin{pmatrix} m_1, \ldots ,m_k \end{pmatrix} + \begin{pmatrix} m^\prime_1, \ldots ,m^\prime_k \end{pmatrix} = \begin{pmatrix} m_1 + m'_1, \ldots ,m_k + m'_k \end{pmatrix}\]And $R$-action given by
\[r \cdot \begin{pmatrix} m_1, \ldots ,m_k \end{pmatrix} = \begin{pmatrix} rm_1, \ldots ,rm_k \end{pmatrix}\]Definition 100. Let $M$ an $R$-module. A subset $N \subseteq M$ an $R$-submodule if it is a subgroup of $(M, + , 0_{M})$ and if $n \in N, r\in R \implies rn \in N$. Write $N \leq M$
Definition 101. *Let $N \leq M$ be an $R$-submodule. The quotient module $M / N$ the set of $N-$cosets in $(M, + , 0_{M}$ with $R$-action given by \(r \cdot (m + N) = (r \cdot m) + N\)
Definition 102. *Function $f: M \to N$ between $R$- modules an $R$- module homomorphism if it is a homomorphism of abelian groups and satisfies
\[f(r \cdot m) = r \cdot f(m), \quad \forall r \in R, m \in M\]An isomorphism, is a bijective homomorphism.
Say 2 $R$- modules are isomorphic if there exists isomorphism between them.*
Definition 103. *If $R_1, R_2$ rings, $M_1$ an $R_1$-module and $M_2$ an $R_2$-module, then $(M_1 \times M_2)$ is a $(R_1 \times R_2)$-module with action
\[(r_1,r_2) \cdot (m_1,m_2) := (r_1m_2, r_2 m_2)\]Definition 104. *$R$ a commutative ring, $S \subseteq R$ a multiplicative submonoid, $M$ an $R$-module.
Localisation of $M$ by $S$,
This an $S^{-1} R$-module, with natural structure of abelian group, and $S^{-1} R$ action given by
\[(r,t) \cdot (m,s) := (rm,ts)\ (r,t) \in S^{-1} R , (m,s) \in S^{-1} M\]Given ideal $I \subseteq R$ localisation $S^{-1} I \subset S^{-1} R$ as an ideal is isomorphism as an $S^{-1} R$-module to the localisation of $I$ as a module.*
Basic theory of modules
THEOREM NUMBERS AND DEFS TO BE AMENDED
Theorem 105. (1st isomorphism theorem)
Let $f: M \to N$ an $R$-module homomorphism, Then we have
$\mathop{ker}(f) = {m \in M: f(m) = 0} \leq M$ (is an R-submodule)
$\mathop{im}(f) = {f(m): m \in M} \leq N$ (is an R-submodule)
Then $M / \mathop{ker}(f) \cong \mathop{im}(f)$
Definition 106. *Let $f: M \to N$ a map of $R$-modules. We define the cokernel of $f$ as
\(\mathop{coker}(f) = N / \mathop{im}(f)\)*
Remark 107. *For submodules, $A_1, \ldots , A_{n}$
\[A_1 + \ldots + A_{n} = \{a_1 + \cdots + a_{n}: a_{i} \in A_{i}\} \leq M \ \text{(an }R\text{-submodule)}\]Theorem 108. (2nd isomorphism theorem)
Let $M$ an $R$-module, let $A,B \leq M$ then
$A+ B := {a+b: a\in A, b\in B}$
$A \cap B \leq M$
*Then
\(\frac{A+B}{A} \cong \frac{B}{A \cap B}\)*
Theorem 109. (3rd isomorphism theorem)
Let $M$ an $R$-module, and $N \leq L \leq M$, Then:
$L / N \leq M / N$
$M / L \cong \frac{M / N}{L / N}$
Definition 110. *$M$ an $R$-module, $m \in M$, submodule generated by $m$ is
\(Rm:= \{r \cdot m : r \in R\} \leq M\)*
Definition 111. *$M$ an $R$-module, $m \in M$, the annihilator of $m$ is
\[\mathop{Ann}(m) := \{r\in R: r \cdot m = 0\}\]Since $\mathop{Ann}(m) = \mathop{ker}(\varphi )$ for the homomorphism
\[\varphi \colon R \to M, r \mapsto r \cdot m\]by 1st isomorphism theorem, we have $\mathop{Ann}(m) \leq R, Rm \cong R / \mathop{Ann}(m)$*
example Example 112. *$R$ a PID, let $I \subseteq R$ an ideal. Then
\[I \cong R\]as $R$-modules.*
Definition 113. $R$-module, $M$ is finitely generated if $\exists m_1, \ldots , m_{n}$ s.t
\[\begin{aligned} M &= Rm_1 + Rm_2 + \ldots + Rm_{n}\\ &= \{r_{1}m_1 + \ldots + r_n m_n: r_1, \ldots , r_{n} \in R \} \end{aligned}\]Lemma 114. $M$ an $R$-module, then $M$ is finitely generated $\iff$ $\exists$ surjective $R$-module homomorphism $f: R^n \to M$ for some $n$
Corollary 115. Let $N \leq M$ be $R$-modules, if $M$ finitely generated, then $M / N$ is finitely generated.
Free and projective modules
Definition 116. *Given set $S$ define the free module over $S$ to be $R$-module
\[R^{(S)} = \bigoplus_{i \in S} R = \{(x_{i})_{i \in S} \in \prod\limits_{s\in S} R : x_{i} = 0 \text{ for all but finitely many } i \}\]with coordinate wise addition and $R$-action.
An $R$-module $M$ is free if $M \cong R^{(S)}$ for some $S$*
Proposition 117. The free module $R^{(S)}$ is finitely generated $\iff S$ finite
Proposition 118. $F$ a field.If $M$ an $F-$module, then $M$ a free $F-$module
Definition 119. $S \subseteq M$ generates $M$ freely if
$S$ generates $M$ as an $R$-module, i.e. $R \cdot S = M$
Any set function $\psi : S \to N$, $N$ a $R$-module, extends to an $R$-module map $\theta :M \to N$
Definition 120. $R$-module $M$ is free, if it is freely generated by some subset $S \subseteq M$. A set $S$ with this property called a basis for $M$
Proposition 121. The two definitions of free module are equivalent
Lemma 122. Suppose $M, N$ are $R$-modules, s.t $M$ freely generated by $S \subseteq M$ and $N$ freely generated by $T \subseteq N$.
If $\exists$ bijection, $S \cong T$ then $M \cong N$ as $R$-modules
Definition 123. Let $m1, \ldots ,m_{n} \in M \implies {m_1, \ldots ,m_{n} }$ is linearly independent if
\[\sum_{i=1}^{n} r_{i}m_{i}=0\]$\implies r_1 = r_2 = \ldots = r_{n} = 0$
Proposition 124. For a subset $S = {m1, \ldots ,m_{n} }\subseteq M$, following are equivalent;
(i) $S$ generates $M$ freely, equivalent to $M \cong R^n$
(ii) $S$ generates $M$ and $S$ is linearly independent
(iii) *Every element of $M$ is uniquely expressible as
\[r_1 m_1 + r_2 m_2 + \ldots r_{n}m_{n}\]for some $r_{i}\in R$*
Definition 125. $M$ a finitely generated $R$-module. We have show that $\exists \varphi : R^n \to M$ a surjective $R$-module homomorphism, for some $n$.
Call the $R$-submodule $ker(\varphi ) \leq R^n$ the *relation module for those generators*
Definition 126. A finitely generated $R$-module $M$ is *finitely presented if there exists a surjective homomorphism $f: R^n \to M$ such that $ker(f)$ a finitely generated $R$-module*
Proposition 127. Let $\varphi :R^m \to R^n$ an $R$-module homomorphism
Let $e_1, \ldots , e_{m} \in R^m$ and $v_1, \ldots ,v_{n}\in R^n$ the standard basis elements
Let $\varphi (e_{j}) = \sum_{i=1}^{n} A_{ij} e_{i}$ for some $A_{ij} \in R$ and let $A = (A_{ij} ) \in M_{m\times n}(R)$ the corresponding $n \times m$ matrix
Then $\varphi (r) = A \cdot r$
Definition 128. Say a ring $R$ has the invariant basis number property (IBN) if $R^n \cong R^m$ are isomorphic as $R$-modules $\iff n = m$
Proposition 129. Non-trivial commutative rings have the invariant basis number property
Definition 130. An $R$-module $M$ is *stably free if there exists $n$ such that $M \oplus R^n$ is a free module
An $R$-module $M$ is projective if there exists an $R$-module $N$ such that $M \oplus N$ is a free $R$-module*
Noetherian modules
Theorem 131. An $R$-module $M$ is Noetherian $\iff$ every $R$-submodule of $M$ is finitely generated.
Corollary 132. R a PID $\implies$ R is Noetherian
Theorem 133. Any finitely generated module over a Noetherian ring is Noetherian
Proposition 134. $M$ a Noetherian $R$-module, then $\forall$ submodules $N \leq M$, both $N$ and $M / N$ are Noetherian
Proposition 135. Let $M$ an $R$-module, let $N$ a Noetherian submodule of $M$, and suppose that $M / N$ is Noetherian. Then $M$is Noetherian
Corollary 136. If $M,N$ are Noetherian $R$-modules, then so is $M \oplus N$
Corollary 137. If $R$ is Noetherian, then any free $R$-module of finite rank is Noetherian
Corollary 138. Let $R$ a Noetherian ring. Then every finitely generated $R$-module is finitely presented
Modules over principal ideal domains
Theorem 139. *(Classification of finitely generated modules over a PID)
Let $R$ a PID. If $M$ finitely generated $R$-module, then $\exists n,r \geq 0$ and elements $d_1, \ldots ,d_{r}\in R$ such that
We can assume that $d_1 \mid d_2 \mid \ldots \mid d_{r}$
Can be shown that is we choose the $d_{i}$ to satisfy these conditions, then the $n$ and $d_{i}$ are unique.