Applied Probability - Concise Notes

MATH60045

PDFs

Problem Sheets

Table of contents

Discrete-time Markov Chains
Properties of the Exponential Distribution
Poisson Process
Continuous-time Markov Chains
Brownian Motion

Discrete-time Markov Chains

Definition of discrete time Markov Chains

Definition 1. A discrete-time stochastic process $X = {X_n}{n \in \mathbb{N}{0} }$ taking values in countable state space $E$ a Markov chain if it satisfies the Markov condition

\[P(X_{n} = j \mid X_{n-1} = i, X_{n-2} = x_{n-2} , \ldots , X_{0} = x_0) = P(X_{n} = j \mid X_{n-1} = i), \forall n \in \mathbb{N}\ \forall x_0, \ldots , x_{n-2}, i ,j \in E\]

Definition 2. (Time Homogenous)

Markov Chain ${X_{n}}_{n \in \mathbb{N}_{0}}$ is time-homogenous if
\[P(X_{n+1} = j \mid X_{n} = i ) = P(X_1 = j \mid X_0 = i),\ \forall n \in \mathbb{N}_0, i,j \in E\]
Transition matrix $P = (p_{ij} )_{i,j\in E}$ is the $K \times K$ matrix of transition probabilities

Definition 3. (Stochastic Matrix)
A square matrix $P$ a stochastic matrix if

$p_{ij} \geq 0, \forall i,j$
$\sum_{j} p_{ij} =1\ \forall i$

Theorem 4. Transition matrix $P$ is stochastic

The $n$-step transition probabilities and Chapman-Kolmogorov equations

Definition 5. $n \in \mathbb{N}$, we have*

\[P_{n} = (p_{ij} (n)) = P(X_{m+n} = j, X_{m}=i),\ m \in \mathbb{N}_0\]

The matrix of $n$-step transition probabilities.

Lemma 6. For discrete markov chain ${X_{n}}_{n \geq 0}$ on state space $E$ we have

\[P(X_{n+m} = x_{n+m} \mid X_{n} = x_{n}, \ldots , X_0 = x_0 ) = P(X_{n+m} = x_{n+m} \mid X_{n} = x_{n}),\ m \in \mathbb{N}, \forall x_{n+m}, x_{n}, \ldots , x_0 \in E\]

Theorem 7. Let $m\in \mathbb{N}_0, n \in \mathbb{N}$ Then we have $\forall i,j \in E$

\[p_{ij } (m+n) = \sum_{l\in E} p_{il}(m) p_{lj} (n) \quad P_{m+n} = P_{m}P_{n} \quad P_{n} = P^n\]

Remark 8. Extend definition for case $K = \infty$
Let $\mathbf{x}$ a $K$-dimensional row vector, $P$ a $K \times K$ matrix

\[(\mathbf{x} P)_{j} := \sum_{i\in E} x_{i} p_{ij}, \quad (P^{2})_{ik} := \sum_{j\in E} p_{ij} p_{jk}, \ i,j,k \in \mathbb{N}\]

Define $P^n$ similarly and take $(P^0){ij} = \delta{ij}$

Dynamics of a Markov Chain

Definition 9. Denote probability mass function of $X_{n}$ for $n \in \mathbb{N}_0$ by

\[\nu_{i}^{(n)} = P(X_{n} = i),\ i \in E\]

Take $K = \mathop{card}(E)$, denote by $\mathbf{\nu}^{(n)}$ the $K$-dimensional row vector with elements $\nu_{i}^{n}, i \in E$
Call this the marginal distribution of chain at time $n \in \mathbb{N}_0$

Theorem 10. We have

\[\mathbf{\nu}^{(m+n)} = \mathbf{\nu}^{(m)}P_{n}= \mathbf{\nu}^{(m)}P^{n},\ \forall n \in \mathbb{N}, m \in \mathbb{N}_0\]

\[\mathbf{\nu}^{(n)} = \nu^{(0)} P_{n} = \mathbf{\nu}^{(0)} P^{n},\ \forall n \in \mathbb{N}\]

Theorem 11. Let $X = {X_{n}}{n \in \mathbb{N}{0}}$ a Markov chain on countable state space $E$

Then given initial distribution $\mathbf{\nu}^{(0)}$ and transition matrix $P$, we determine all finite dimensional distributions of Markov chain.

$\forall 0 \leq n_1 < n_2 < \cdots < n_{k-1} < n_{k} \ (n_{i} \in \mathbb{N}_0, i = 1, \ldots ,k ), k \in \mathbb{N}, x_1, \ldots ,x_k \in E$

We have

\[\begin{aligned} P(X_{n_1} = x_1, X_{n_2} = x_2, \ldots , X_{n_{k}} = x_{k}) &= (\mathbf{\nu}^{(0)}P^{n_1})_{x_1} (P^{n_2 - n_1})_{x_1 x_2} \cdots (P^{n_{k} - n_{k-1}})x_{k-1} x_{k}\\ &= (\mathbf{\nu}P^{n_1})x_1 p_{x_1 x_2}(n_2 - n_1) \cdots p_{x_{k-1} x_{k}}(n_{k}-n_{k-1} ) \end{aligned}\]

First passage/hitting times

Definition 12. Define first passage/hitting time of $X$ for state $j \in E$ as

\[T_{j} = \mathop{\min} \{n \in N: X_{n}=j\}\]

If $X_{n} \neq j, \forall n \in \mathbb{N}$ then set $T_{j} = \infty$

Definition 13. *For $i,j \in E, n \in \mathbb{N}$ define first passage probability

\[f_{ij} (n) = P(T_{j} = n \mid X_0 = i) = P(X_{n} = j, X_{n-1} \neq j, \ldots , X_1 \neq j \mid X_0 = i)\]

Probability that we visit state $j$ at time $n$, given we start at $i$ at time $0$

Define $f_{ij} (0) = 0, f_{ij} (1) = p_{ij} , \forall i,j \in E$

Definition 14. Define

\[f_{ij} = P(T_{j} < \infty \mid X_0 = i)\]

For $i \neq j$, we have $f_{ij}$ the probability that the chain ever visits state $j$, starting at $i$

Call $f_{ii}$ the returning probability*

Proposition 15. $\forall i,j \in E$

\[f_{ij} = \sum_{n=1}^{\infty} f_{ij} (n)\]

Lemma 16. $\forall i,j \in E, n \in \mathbb{N}$, we have

\[\begin{aligned} p_{ij} (n) &= \sum_{l=0}^{n} f_{ij} (l) p_{jj}(n-l)\\ &= \sum_{l=1}^{n} f_{ij} (l) p_{jj}(n-l) \end{aligned}\]

Recurrence and transience

Definition 17. Let ${X_{n}}{n \in \mathbb{N}{0}}$ be a markov chain on countable state space $E$.

\[j \in E,\ P(X_{n}=j,\text{for some } n \in \mathbb{N}\mid X_0 = j ) = f_{jj} \begin{cases} 1, &\text{ recurrent} ;\\ <1, &\text{ transient } . \end{cases}\]

Theorem 18. $j \in E$

\[\sum_{n=1}^{\infty} p_{ij} (n) = \begin{cases} \infty , & \iff \text{ recurrent } ;\\ < \infty , & \iff \text{ transient } . \end{cases}\]

Define

\[N_{j} = \sum_{n=0}^{\infty } I_{n}^{(j)}, \quad I_{n}^{(j)} = I_{X_n = j} = \begin{cases} 1, &\text{ if } X_{n} = j ;\\ 0, &\text{ if } X_{n}\neq j . \end{cases}\]

Theorem 19. $j \in E$ transient*

$P(N_{j} = n \mid X_0 = j) = f_{jj}^{n-1} (1 - f_{jj})$ for $n \in \mathbb{N}$ geometric distribution with param $f_{jj}$
$i \neq j$

\[P(N_{j} = n \mid X_0 = i) = \begin{cases} 1 - f_{ij} , &\text{ if } n=0 ;\\ f_{ij} f_{jj}^{n-1}(1-f_{jj}), &\text{ if } n \in \mathbb{N} . \end{cases}\]

Corollary 20. $j \in E$ transient

\[E(N_{j}\mid X_0 = j) = \frac{1}{1-f_{jj}}\]
$i \neq j$ we have
\[E(N_{j} \mid X_0 = i) = \frac{f_{ij}}{1 - f_{jj}}\]

Theorem 21. *Given $X_0 = j$, we have

\[E(N_{j} \mid X_0 = j) = \sum_{n=0}^{\infty} p_{jj}(n)\]

Sum may diverge to $\infty$

Corollary 22. $j \in E$ transient then $p_{ij} (n) \xrightarrow[n\to \infty]{} 0, \forall i \in E$

Mean recurrence time, null and positive recurrence

Definition 23. The mean recurrence time $\mu_{i}$ of state $i \in E$ defined as $\mu_{i} = E[T_{i} \mid X_0 = i]$

Theorem 24. *Let $i \in E$. We have $P(T_{i} = \infty \mid X_0 = i) > 0$ $\iff i$ transient, where we get

\[\mu_{i} = E[T_{i} \mid X_0 = i = \infty ]\]

Theorem 25. *For recurrent state $i \in E$ we have

\[\mu_{i}= E[T_{i}\mid X_0 = i] = \sum_{n=1}^{\infty} n f_{ii}(n)\]

Can be finite or infinite.

Definition 26. *A recurrent state $i \in E$

\[\mu_{i} = \begin{cases} \infty , &\text{ called } \textbf{null} ;\\ < \infty , &\text{ called } \textbf{positive} . \end{cases}\]

Theorem 27. *Recurrent state $i \in E$ null $\iff$ $p_{ii}(n) \xrightarrow[n\to \infty ]{} 0$
Further, if this holds, then $p_{ji} (n) \xrightarrow[n\to \infty ]{} 0 , \forall j \in E$

Generating functions for $p_{ij} (n), f_{ij} (n)$ (READING MATERIAL)

Example: Null recurrence/transience of a simple random walk (READING MATERIAL)

\[SEE\ FULL\ OFFICIAL\ NOTES\]

Aperiodicity and ergodicity

Definition 28. Period of state $i$ defined by

\[d(i) = gcd\{n : p_{ii}(n) > 0\}\]

Definition 29. A state ergodic if it is positive recurrent and aperiodic

Communicating classes

Definition 30. (Accessible and Communicating)

$j$ accessible from $i$, $i \to j$, if $\exists m \in \mathbb{N}0$ s.t $p{ij} (m) >0$
$i, j$ communicate, if $i \to j$ and $j \to i$; write $i \leftrightarrow j$

Theorem 31. (Communication an equivalence relation)
Satisfies, reflexivity, symmetry and transitivity

Theorem 32. If $i \leftrightarrow j$ then

$i,j$ have same period
$i$ transient/recurrent $\iff$ $j$ transient/recurrent
$i$ null recurrent $\iff$ $j$ null recurrent

Definition 33. Set of states $C$ is

*closed if $\forall i \in C, j \notin C, p_{ij} - 0$
*irreducible if $i \leftrightarrow j, \forall i,j \in C$

Theorem 34. Let $C$ a closed communicating class, transition matrix $P$ restricted to $C$ is stochastic

The decomposition theorem

Theorem 35. $C$ a communicating class, consisting of recurrent states. Then $C$ is closed*

Theorem 36. *State-space $E$ can be partitioned uniquely into

\[E = \underbrace{T}_{\text{transient states} } \cup \left( \bigcup\limits_{i} \underbrace{C_{i}}_{\substack{\text{irreducible, closed}\\ \text{set of recurrent states}} } \right)\]

Theorem 37. $K < \infty$ Then at least one state is recurrent and all recurrent states are positive.

Theorem 38. $C$ a finite, closed communicating class $\implies$ all states in $C$ positive recurrent

Class properties

Type of Class	Finite	Infinite
Closed	positive recurrent	positive recurrent, null recurrent, transient
Not Closed	transient	transient

Application: The gambler’s ruin problem

The problem and the results

Consider a gambler with initial fortune $i \in {0,1, \ldots , N}$. At each play of the game, the gambler has

probability $p$ of winning one unit
probability $q$ of losing one unit
each successive game is independent

What is the probability, a gambler starting at $i$ units, has their fortune reach $N$ before $0$ ?

Let $X_{n}$ denote gamblers fortune at time $n$. Then ${X_{n}}{n \in \mathbb{N}{0}}$ is a Markov Chain with transition probabilities, shown in diagram above.

This yields 3 communicating classes.

\[\underbrace{C_1 = \{0\}, C_2 = \{N\}}_{\substack{\text{positive recurrent}\\ \text{since finite and closed} } }, T_1 = \{1,2, \ldots , N-1\}\]

Define the following for our problem:
Define first time $X$ visits state $i$ as

\[V_{i} = \mathop{\min} \{n \in \mathbb{N}_0 : X_{n} = i\}\] \[h_{i} = h_{i}(N) = P(V_{N}< V_0 \mid X_0 = i)\]

This yields the following recurrence relation

\[h_{i} = h_{i+1} p + h_{i-1} q,\ i = 1,2, \ldots , N-1\]

Theorem 39. From above we achieve

\[h_{i}= h_{i}(N) = \begin{cases} \frac{1-(q /p)^i}{1 - (q /p)^N}, &\text{ if } p \neq \frac{1}{2} ;\\ \frac{i}{N}, &\text{ if } p = \frac{1}{2} . \end{cases}\]

Theorem 40. *We also have

\[\lim\limits_{N \to \infty} h_{i}(N) = h_{i}(\infty ) = \begin{cases} 1 - (q /p)^i, &\text{ if } p > \frac{1}{2} ;\\ 0, &\text{ if } p \leq \frac{1}{2} . \end{cases}\]

$p > \frac{1}{2} \implies \frac{q}{p} < 1 \implies \lim\limits_{N \to \infty} (\frac{q}{p})^N = 0$
$p < \frac{1}{2} \implies \frac{q}{p} > 1 \implies \lim\limits_{N \to \infty} = \infty$

Stationarity

Definition 41. (Distributions)

row vector $\mathbf{\lambda}$ a distribution on $E$ if
\[\forall j \in E, \lambda_{j} \geq 0,\ \text{ and } \sum_{j\in E} = 1\]
row vector $\mathbf{\lambda}$ with non-negative entries is called invariant for transition matrix $P$ if $\lambda P = \lambda$
row vector $\mathbf{\pi}$ is invariant/stationary/equilibrium distribution of Markov chain on $E$ with transition matrix $P$ if
1. $\mathbf{\pi}$ a distribution
2. it is invariant
\[\pi P^n = \pi\]

Stationarity distribution for irreducible Markov Chains

Theorem 42. *An irreducible chain has stationary distribution $\pi$ $\iff$ all states are positive recurrent.
$\pi$ unique stationary distribution, s.t $\pi_i = \mu_{i}^{-1} \forall i$

Lemma 43. *For markov chain $X$ we have $\forall j \in E, n, m \in \mathbb{N}$

\[f_{jj}(m+n) = \sum_{i\in E, i \neq j} l_{ji} (m) f_{ij} (n)\]

For $l_{ji} (n) = P(X_{n} = i. T_{j} \geq n \mid X_0 = j)$

Corollary 44. *For Markov Chain $X$ we have $\forall i,j \in E, i \neq j$ and $\forall n,m \in \mathbb{N}$

\[f_{jj}(m+n) \geq l_{ji} (m) f_{ij} (n)\]

Lemma 45. *Let $i \neq j$ Then $l_{ji} (1) = p_{ji}$, and for integers $n \geq 2$

\[l_{ji} (n) = \sum_{r\in E: r \neq j} p_{ri} l_{jr} (n-1)\]

Lemma 46. $\forall j \in E$ of an irreducible, recurrent chain, the vector $\mathbf{\rho}(j)$ satisfies $\rho_{i}(j) < \infty\ \forall i$ and further $\mathbf{\rho} (j) = \mathbf{\rho} (j)P$

Lemma 47. Every irreducible, positive, recurrent chain has a stationary distribution

Theorem 48. If the chain is irreducible and recurrent, then $\exists \mathbf{x} > 0$ s.t $\mathbf{x} = \mathbf{x} \mathbf{P}$ unique up to multiplicative constant.

\[\text{Chain is } \begin{cases} \text{positive recurrent}, &\text{ if } \sum_{i}x_{i} < \infty ;\\ \text{null} , &\text{ if } \sum_{i}x_{i} = \infty . \end{cases}\]

Lemma 49. Let $T$ a non-negative integer valued random variable on probability space $(\Omega ,\mathcal{F} ,P)$, with $A \in \mathcal{F}$ an event s.t $P(A) > 0$. Can show that

\[E(T\mid A) = \sum_{n=1}^{\infty} P(T \geq n \mid A)\]

Theorem (Dominated convergence theorem)

Let $\mathcal{I}$ be a countable index set.
If $\sum_{i \in \mathcal{I}} a_{i}(n)$ is an absolutely convergent series $\forall n \in N$ s.t

$\forall i \in \mathcal{I}$ the limit $\lim\limits_{n \to \infty} a_{i}(n) = a_{i}$ exists
$\exists$ seq. $(b_{i}){i\in I}$ s.t $b{i} \geq 0\, \forall i$ and $\sum_{i\in \mathcal{I}} b_{i} < \infty$ s.t $\forall n, i: \mid a_{i}(n)\mid \leq b_{i}$

Then $\sum_{i\in \mathcal{I}} \mid a_{i} \mid < \infty$ and

\[\sum_{i\in I}a_{i} = \sum_{i\in I} \lim\limits_{n \to \infty} a_{i}(n) = \lim\limits_{n \to \infty} \sum_{i\in \mathcal{I}}a_{i}(n)\]

Limiting distribution

Definition 50. A distribution $\pi$ is the limiting distribution of a discrete-time Markov Chain if, $\forall i,j \in E$ we have

\[\lim\limits_{n \to \infty} p_{ij} (n) = \pi_{j}\]

Definition 51. For irreducible aperiodic chain we have

\[\lim\limits_{n \to \infty} p_{ij} (n) = \frac{1}{\mu_{j}}\]

Ergodic Theorem

Theorem 52. *(Ergodic Theorem)
Suppose we have irreducible Markov chain ${X_{n}}{n \in \mathbb{N}{0}}$ with state space $E$. Let $\mu_{i}$ the mean recurrence time to state $i \in E$

\[V_{i}(n) = \sum_{k=0}^{n-1} \mathbf{1}_{\{X_{k}=i\}}\]

The number of visits to $i$ before $n$

So we have $V_{i}(n) / n$ the proportion of time before $n$ spent at $i$

\[P \left(\frac{V_{i}(n)}{n}\to \frac{1}{\mu_{i}}, \text{ as } n \to \infty\right) = 1\]

Summary: Properties of irreducible Markov Chains
3 kinds of irreducible Markov Chains

Positive recurrent
1. Stationary distribution $\pi$ exists
2. Stationary distribution is unique
3. All mean recurrence times are finite and $\mu_{i} = \frac{1}{\pi_i}$
4. $V_{i}(n) / n \xrightarrow[n \to \infty ]{} \pi_i$
5. If chain aperiodic
  \[\lim\limits_{n \to \infty} P(X_{n} = i) = \pi_i, \forall i \in E\]
Null recurrent
1. Recurrent, but all mean recurrence times are infinite
2. No stationary distribution exists
3. $V_{i}(n) / n \xrightarrow[n \to \infty ]{} 0$
4. \[\lim\limits_{n \to \infty} P(X_{n} = i) = 0, \forall i \in E\]
Transient
1. Any particular state is eventually never visited
2. No stationary distribution exists
3. $V_{i}(n) / n \xrightarrow[n \to \infty ]{} 0$
4. \[\lim\limits_{n \to \infty} P(X_{n} = i) = 0, \forall i \in E\]

Properties of the elements of a stationary distribution associated with transient or null-recurrent states

Theorem 53. *Let $X$ a time-homogeneous Markov Chain on countable state space $E$
If $\pi$ a stationary distribution of $X$, $i \in E$ either transient or null-recurrent, then $\pi_i = 0$

Existence of a stationary distribution on a finite state space

Theorem 54. If state space finite $\implies \exists$ at least one positive recurrent communicating class

Theorem 55. Suppose finite state space. The stationary distribution $\pi$ for transition matrix $P$ unique $\iff$ there is a unique closed communicating class

Corollary 56. Markov chain on finite state space, and $N \geq 2$ closed classes.
$C_{i}$ the closed classes of Markov chain and $\pi^(i)$ the stationary distribution associated with class $C_{i}$ using construction

\[\pi_{j}^{(i)} = \begin{cases} \pi_{j}^{C_{i}}, &\text{ if } j \in C_{i} ;\\ 0 , &\text{ if } j \notin C_{i} . \end{cases}\]

Then every stationary distribution of Markov Chain represented as

\[\sum_{i=1}^{N} \omega_{i}\pi^{(i)}\]

For weights $\omega_{i} \geq 0, \sum_{i=1}^{n} \omega _{i} = 1$

Limiting distributions on a finite state space

Theorem 57. *Let $K = \mid E\mid < \infty$ Suppose for some $i \in E$ that

\[\lim\limits_{n \to \infty} p_{ij} (n) = \pi_{j}, \quad \forall j \in E\]

Then $\pi$ a stationary distribution*

Time reversibility

Theorem 58. *For irreducible, positive recurrent Markov chain ${X_{n}}_{n \in 0,1, \ldots , N }, N \in \mathbb{N}$ assume $\pi$ a stationary distribution, and $P$ a transition matrix, and $\forall n \in {0,1, \ldots , N}$ the marginal distribution $\nu^{(n)}= \pi$

\[Y_{n} = X_{N-n}, \quad \text{The reversed chain defined for } n \in \{0,1, \ldots , N\}\]

We have $Y$ a Markov chain, satisfying

\[P(Y_{n+1} = j \mid Y_{n} = i) = \frac{\pi_{j}}{\pi_i}p_{ji}\]

Definition 59. $X = {X_{n}: n \in {0,1, \ldots , N}}$ an irreducible Markov chain with stationary distribution $\pi$ and marginal distributions $\nu^{(n)} = \pi,\ \forall n \in {0,1, \ldots , N}$
Markov chain $X$ time-reversible if transition matrices of X and its reversal $Y$ are the same.*

Theorem 60. ${X_{n}}_{n \in {0,1, \ldots , N}}$ time-reversible $\iff, \forall i,j \in E$

\[\pi_i p_{ij} = \pi_{j}p_{ji}\]

Theorem 61. For irreducible chain, if $\exists \pi$ s.t *3.10.1 holds $\forall i,j \in E$. Then the chain is time-reversible (once in its stationary regime) and positive recurrent with stationary distribution $\pi$

Properties of the Exponential Distribution

Definition and basic properties

Definition 62. *(Exponential distribution)
A continuous random variable $X$ is $X \sim Exp(\lambda )$ if it has density function

\[f_{X}(x) = \begin{cases} \lambda e^{-\lambda x}, &\text{ if } x>0 ;\\ 0, &\text{ if } \text{otherwise} . \end{cases}\]

Cumulative distribution function

\[F_{X}(x) = \begin{cases} 0, &\text{ if } x \leq 0 ;\\ 1-e^{-\lambda x}, &\text{ if } x>0 . \end{cases}\]

Survival function of the exponential distribution is given by

\[P(X > x) = \begin{cases} 1, &\text{ if } x \leq 0 ;\\ e^{-\lambda x}, &\text{ if } x > 0 . \end{cases}\]

Theorem 63. $X \sim Exp(\lambda )$ for $\lambda > 0$ Then*

$E(X) = \frac{1}{\lambda }$
$\lambda X \sim Exp(1)$

Theorem 64. Let $n \in \mathbb{N}$ and $\lambda > 0$. Consider independent and identically distributed random variables $H_{i}\sim Exp(\lambda )$, for $i = 1, \ldots , n$
Let $J_{n} := \sum_{i=1}^{n} H_{i}$ Then $J_{n}$ follows the Gamma($n,\lambda$) distribution, i.e

\[f_{J_{n}}(t) = \frac{\lambda^n}{\Gamma (n)}t^{n-1}e^{-\lambda t}\]

Theorem 65. Let $n \in \mathbb{N}$ and $\lambda_1, \ldots , \lambda_n$. Consider independent random variables $H_{i} \sim Exp(\lambda_{i})$ for $i = 1, \ldots , n$. Let $H := \mathop{\min} {H_1, \ldots , H_{n}}$ Then

$H \sim Exp(\sum_{i=1}^{n} \lambda i)$
*For any $k = 1, \ldots , n, P(H = H_{k}) = \lambda_{k} / \sum_{i=1}^{n} \lambda_{i}$

Theorem 66. *Consider a countable index set $E$ and ${H_{i}: i \in E}$ independent random variables with $H_{i} \sim Exp(\lambda_{i}), \forall i \in E$. Suppose that $\sum_{i\in E} \lambda_{i}< \infty$ and set $H := \inf_{i\in E} H_{i}$
Then the infimum is attained at a unique random value $I$ of $E$ with probability $1$
$H, I$ are independent, with $H \sim Exp(\sum_{i\in E}\lambda_{i} < \infty)$ and $P(I = i) = \lambda_{i} / \sum_{k\in E} \lambda_{k}$

Remark 67. *Suppose we have $X \sim Exp(\lambda_{X}), Y \sim Exp(\lambda_{Y})$, Then

\[P(X < Y) = P(\mathop{\min}\{X,Y\} = X) = \frac{\lambda_{X}}{\lambda_{X} + \lambda_{Y}}\]

Lack of memory property

Theorem 68. *(Lack of memory property)
A continuous random variable $X: \Omega \to (0,\infty )$ has an exponential distribution $\iff$ has the lack of memory property

\[P(X > x + y \mid X >x) = P(X >y),\quad \forall x,y > 0\]

Remark 69. *A random variable $X: \Omega \to (0,\infty )$ has an exponential distribution $\iff$ has lack of memory property:

\[P(X > x + y \mid X >x) = P(X >y),\quad \forall x,y > 0\]

Criterion for the convergence/divergence of an infinite sum of independent exponentially distributed random variables

Theorem 70. Consider sequence of independent random variables $H_{i}\sim Exp(\lambda_{i})$ for $0 < \lambda_{i}< \infty$ for all $i \in \mathbb{N}$ and let $J_\infty = \sum_{i=1}^{\infty} H_{i}$, Then:

*If $\sum_{i=1}^{\infty} \frac{1}{\lambda_{i}} < \infty \implies P(J_\infty < \infty ) = 1$
*If $\sum_{i=1}^{\infty} \frac{1}{\lambda_{i}} = \infty \implies P(J_\infty = \infty ) = 1$

Lemma 71. *For $x \geq 1$, we have

\[\log \left( 1 + \frac{1}{x} \right) \geq \log (2)\frac{1}{x}\] \[\log (1+x) > \frac{x}{x+1}, \quad \text{for } x > -1\]

Poisson Process

Remarks on continuous-time stochastic processes on a countable state space

Some Definitions

Definition 72. A stochastic process ${N_{t}}_{t \geq 0}$ a counting process if $N_{t}$ represents the total number of ‘events’ that have occurred up to time $t$
Having the following properties:

$N_0 = 0$
$\forall t \geq 0, N_{t}\in \mathbb{N}_0$
*If $0 \leq s \leq t, N_{s} \leq N_{t}$
*For $s < t, N_{t} - N_{s} =$ the number of events in interval $(s,t]$
*Process is piecewise constant and has upward jumps of size 1 i.e $N_{t} - N_{t-} \in {0,1}$

Definition 73. *Let $(J_{n}){n \in \mathbb{N}_0}$ a strictly increasing sequence of positive random variables s.t $J_0 = 0$ almost surely.
Define process ${N{t}}_{t \geq 0}$ as

\[N_{t} = \sum_{n=1}^{\infty} \mathbf{1}_{\{J_{n}\leq t\}} ,\]

Interpret $J_{n}$ as the (random) time at which the $n$th event occurs.
The $n$th jump time.*

Poisson Process: First Definition

Definition 74. *Define $o(\cdot )$ notation.
A function $f$ is $o(\delta )$ if

\[\lim\limits_{\delta \downarrow 0} \frac{f(\delta )}{\delta } = 0\]

With the following properties*

if $f,g$ are $o(\delta )$ then so is $f + g$
if $f$ is $o(\delta )$ and $c \in \mathbb{R}$ then $cf$ is $o(\delta )$

Definition 75. A Poisson process ${N_{t}}_{t \geq 0}$ of rate $\lambda >0$ is a non-decreasing stochastic process with values in $\mathbb{N}_0$ satisfying:

$N_0 = 0^1$
Increments are independent, that is given any $n \in \mathbb{N}$ and $0 \leq t_0 < t_1 < t_2 < \ldots < t_n$ random variables $N_{t_0}, N_{t_1} - N_{t_0}, N_{t_2} - N_{t_1}, N_{t_3} - N_{t_2}, \ldots , N_{t_n} - N_{t_{n-1}}$ are independent
*The increments are stationary, Given any 2 distinct times $0 \leq s <t, \forall k \in \mathbb{N}_0$
\[P(N_{t}- N_{s} = k) = P(N_{t-s} = k)\]
There is a ‘single arrival’, i.e $\forall t \geq 0, \delta > 0, d \to 0$:
\[\begin{aligned} P(N_{t+\delta } - N_{t} = 1) &= \lambda \delta + o(\delta )\\ P(N_{t+\delta } -N_{t} \geq 2) &= o(\delta ) \end{aligned}\]

Poisson Process: Second definition

Definition 76. A Poisson Process ${N_{t}}_{t \geq 0}$ of rate $\lambda > 0$ is a stochastic process with values in $\mathbb{N}_0$ satisfying

$N_0 = 0$
Increments are independent, that is given any $n \in \mathbb{N}$ and $0 \leq t_0 < t_1 < t_2 < \ldots < t_n$ random variables $N_{t_0}, N_{t_1} - N_{t_0}, N_{t_2} - N_{t_1}, N_{t_3} - N_{t_2}, \ldots , N_{t_n} - N_{t_{n-1}}$ are independent
*The increments are stationary, Given any 2 distinct times $0 \leq s <t, \forall k \in \mathbb{N}_0$
\[P(N_{t}- N_{s} = k) = P(N_{t-s} = k)\]
$\forall t \geq 0, N_{t} \sim \mathop{Poi}(\lambda t)$
\[\forall k \in \mathbb{N}_0, P(N_{t} =k) = \frac{(\lambda t)^k}{k !} e^{-\lambda t}\]

Right-continuous modification

Definition 77. *For 2 stochastic processes ${X_{t}}{t \geq 0},{Y{t}}_{t \geq 0}$, say $X$ a modification of $Y$ if

\[X_{t} = Y_{t},\ \text{almost surely for each} t \geq 0\] \[P(X_{t} = Y_{t}) = 1, \forall t \geq 0\]

Can show that for each Poisson process, $\exists !$ modification which is càdlàg, (right continuous with left limits).*

Remark 78. *Note that the jump chain of the Poisson Process given by $Z = (Z_{n}){n \in \mathbb{N}_0}$, where $Z{n} = n, n \in \mathbb{N}_0$

Equivalence of definitions

Theorem 79. Definition *5.3.3, 5.3.4 are equivalent*

Lemma 80. *Laplace transform of a Poisson random variable of mean $\lambda t, X\sim \mathop{Poi}(\lambda t)$ for $\lambda >0, t>0$ is given by

\[\mathcal{L}_{X}(u) = \exp \{\lambda t[e^{-u} -1]\},\quad \forall u > 0\]

Some properties of Poisson processes

Inter-arrival time distribution

Definition 81. *Let ${N_{t}}_{t \geq 0}$ a Poisson process of rate $\lambda >0$
Then the inter-arrival times are independently and identically distributed exponential random variables with parameter $\lambda$

Time to the $n^{th}$ event

Theorem 82. *We have $\forall n \in \mathbb{N}$, the time to the $n^{th}$ event $J_{n}$ follows a Gamma$n,\lambda$ distribution, with density

\[f_{J_n} (t) = \frac{\lambda^n}{\Gamma (n)}t^{n-1} e^{-\lambda t},\ t > 0\]

Poisson process: Third definition

Definition 83. A Poisson process ${N_t}_{t \geq 0}$ of rate $\lambda > 0$ is a stochastic process with values in $\mathbb{N}_0$ s.t

$H_1,H_2, \ldots$ denote independently and identically exponentially distributed random variables with parameter $\lambda > 0$
*Let $J_0 = 0$ and $J_{n} = \sum_{i=1}^{n} H_{i}$
*Define
\[N_{t} = \sup \{n \in \mathbb{N}_0 : J_{n} \leq t \},\quad \forall t \geq 0\]

Theorem 84. Definitions *5.3.3, 5.3.4, 5.4.4 are equivalent*

Conditional distribution of the arrival times

Theorem 85. *Let ${N_{t}}{t \geq 0}$ be a Poisson process of rate $l > 0$. Then $\forall n \in \mathbb{N}, t > 0$, the conditional density of $\begin{pmatrix} J_1, \ldots ,J_n \end{pmatrix}$ given by $N{t} = n$ is given by

\[f_{\begin{pmatrix} J_1, \ldots ,J_n \end{pmatrix}} \begin{pmatrix} t_1, \ldots ,t_n \mid N_{t}= n\end{pmatrix} = \begin{cases} \frac{n! }{t^n}, &\text{ if } 0 < t_1 < \ldots < t_n \leq t ;\\ 0, &\text{ otherwise } . \end{cases}\]

Remark 86. *The above theorem says, conditional on the fact $n$ events have occured in $[0,t]$, the times $\begin{pmatrix} J_1, \ldots ,J_n \end{pmatrix}$ at which the events occur, when considered as unordered random variables are independently and uniformly distributed on $[0,t]$

Some extensions to Poisson processes

Superposition

Theorem 87. *Given $n$ independent Poisson processes ${N_t^(1)}{t \geq 0}, \ldots , {N{t}^{(n)}}{t \geq 0}$ with respective rates, $\lambda _1, \ldots , \lambda{n}>0$ define

\[N_{t} = \sum_{i=1}^{n} N_{t}^{(i)},\quad t \geq 0\]

Then ${N_{t}}{t \geq 0}$ a Poisson process with rate $\lambda = \sum{i=1}^{n} \lambda_{i}$ and is called a superposition of Poisson processes*

Thinning

Theorem 88. *Let ${N_{t}}{t \geq 0}$ a Poisson process with rate $\lambda > 0$. Assume that each arrival, independent of other arrivals, is marked as a type $k$ event with probability $p{k}$ for $k = 1, \ldots , n$ where $\sum_{i=1}^{n} p_{i} = 1$.
Let $N_{t}^{(k)}$ denote the number of type $k$ events in $[0,t]$ . Then ${N_{t}^{(k)}}{t \geq 0}$ a Poisson process with rate $\lambda p{k}$ and the processes

\[\{N_t^(1)\}_{t \geq 0}, \ldots , \{N_{t}^{(n)}\}_{t \geq 0}\]

are independent. Each process called a thinned Poisson process*

Non-homogeneous Poisson processes

Definition 89. Let $\lambda : [0,\infty) \mapsto (0,\infty )$ denote a non-negative and locally integrable function, called the intensity function
A non-decreasing stochastic process $N = {N_{t}}_{t \geq 0}$ with values in $\mathbb{N}_0$ called a non-homogeneous Poisson process with intensity function $(\lambda (t))_{t \geq 0}$ if it satifies the following:

$N_0 = 0$
$N$ has independent increments*
*‘Single arrival’ property, For $t \geq 0, \delta > 0$
\[\begin{aligned} P(N_{t+\delta } - N_{t} = 1) &= \lambda (t)\delta + o(\delta )\\ P(N_{t+\delta } - N_{t} \geq 2) &= o(\delta ) \end{aligned}\]

*Note that (3) also implies that

\[P(N_{t+\delta } - N_{t} = 0) =1 - \lambda (t) + o(\delta )\]

Theorem 90. *Let $N = {N_{t}}{t \geq 0}$ denote a non-homogeneous Poisson process with continuous intensity function $(\lambda (t)){t \geq 0}$ Then

\[N_{t}\sim \mathop{Poi}(m(t)),\quad \text{where}\quad m(t) = \int_0^t \lambda (s) ds\]

i.e. $\forall t \geq 0, n \in \mathbb{N}_0$

\[P(N_{t}= n) = \frac{[m(t)]^n}{n !}e^{-m(t)}\]

Compound Poisson processes

Definition 91. *Let ${N_{t}}{t \geq 0}$ be a Poisson process of rate $\lambda > 0$.
$Y_1,Y_2, \ldots$ be a sequence of independent and identically distributed random variables, that are independent of ${N{t}}{t \geq 0}$. Then the process ${S{t}}_{t \geq 0}$ with

\[S_{t} = \sum\limits_{i=1}^{N_{i}} Y_{i},\quad t \geq 0\]

is a compound Poisson process*

Theorem 92. *Let ${S_{t}}_{t \geq 0}$ a compound Poisson process. Then for $t \geq 0$

\[E(S_{t}) = \lambda t E(Y_1), \quad Var(S_{t}) = \lambda t E(Y_{1}^{2} )\]

as defined in *Definition 5.5.12**

The Cramér-Lundberg model in insurance mathematics

Definition 93. The Cramér-Lundberg model is given by the following five conditions.

*Claim size process is denoted by $Y = (Y_{k}){k \in \mathbb{N}}$, for $Y{k}$ denoting the positive i.i.d random variables with finite mean $\mu = E(Y)1$ and variance $\sigma^{2} = Var(Y_1) \leq \infty$
*Claim times occur at the random instants of time
\[0 < J_1 < J_2 < \ldots a.s..\]
*The claim arrival process is denoted by
\[N_{t} = \sup \{n \in \mathbb{N}: J_{n} \leq t\}, t \geq 0\]
which is the number of claims in the interval $[0,t]$.*
*The inter-arrival times are denoted by
\[H_1 = J_1, H_{k} = J_{k}- J_{k-1} , k = 2,3, \ldots\]
and are independent and exponentially distributed with parameter $\lambda$
sequences $(Y_{k},(H_{k}))$ are independent of each other

Definition 94. *The Total claim amount is defined as the process $(S_{t})_{t \geq 0}$ satisfying

\[S_{t} = \begin{cases} \sum_{i=1}^{N_{t}} Y_{i}, &\text{ if } N_{t} > 0 ;\\ 0, &\text{ if } N_{t} =0 . \end{cases}\]

Observe that the total claim amount is modelled as a compound Poisson process.*

Theorem 95. *The total claim amount distribution given by

\[P(S_{t}\leq x) = \sum_{n=0}^{\infty} e^{-\lambda t} \frac{(\lambda t)^n}{n !}P \left( \sum_{i=1}^{n} Y_{i} \leq x \right), \quad x \geq 0, t \geq 0\]

and $P(S_{t}\leq x) = 0$ for $x < 0$

Definition 96. *The risk process ${U_{t}}_{t \geq 0}$ is defined as

\[U_{t} = u + ct - S_{t},\quad t \geq 0\]

where $u \geq 0$, the initial capital and $c > 0$ denotes the premium income rate*

Definition 97. *We have the following definitions
*

*The ruin probability in finite time is given by
\[\psi (u,T) = P(U_{t} < 0 \ \text{ for some } t \leq T ),\ 0 < T < \infty, u \geq 0\]
*The ruin probability in infinite time is given by
\[\psi (u) := \psi (u, \infty ), u \geq 0\]

Theorem 98.

\[E(U_{t}) = u + ct - \lambda t \mu + (c - \lambda \mu )t\]

A minimal requirement for choosing the premium could be

\[c > \lambda \mu\]

referred to as the net profit condition*

The coalescent process

Problem

Given collection of $n$ individuals - observe a DNA sequence from the individual
A DNA sequence a collection of letters; A,C,T and G - for simplicity take that only one letter observed
Coalescent process provides genealogical tree representation of this data. A tree-like structure representing the history of the individuals backward in time.
Individuals coalesce until we have only individual - the most recent common ancestor.

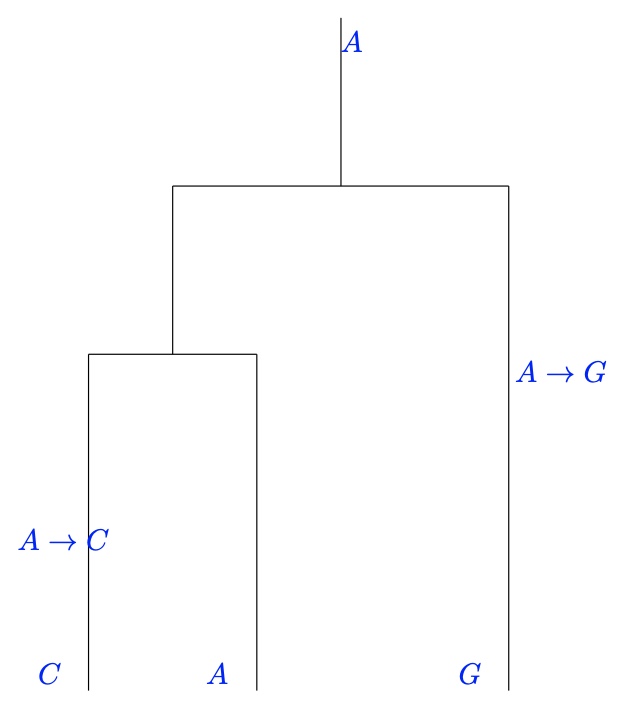
A Coalescent Graph

The Process

At start of process we have $n \geq 2$ individuals (all of the same DNA base)
Each pair of individuals coalesce according to an (independent) Poisson process of rate $1$
We have $\begin{pmatrix} n
2
\end{pmatrix}$ pairs - time to first coalescent event is exponential random variable of rate $\begin{pmatrix} n
2
\end{pmatrix}$ - since we consider the minimum of $\begin{pmatrix} n
2
\end{pmatrix}$ independent $Exp(1)$-distributed random variables.
At first event - 2 individuals picked uniformly at random and combined
Continue this until there is only one individual - the most recent common ancestor
So we have $n-1$ coalescent events
Model, assumes all individuals have the same DNA base, so we require another mechanism - a mutation process
In this process the number of individuals decrease - our first example of a death process.

Time to most recent common ancestor

Time to most recent common ancestor estimated i.e. the height of the tree, estimated by

\[E \left( \sum_{k=1}^{n-1} H_{k} \right), \text{ for } n \in \mathbb{N}, n \geq 2\]

Where we have that $H_{k}$ the time to $k^{th}$ coalescence

\[H_{k} \sim \text{Exp} \left( \begin{pmatrix} n - (k-1) \\ 2 \\ \end{pmatrix} \right) \implies E(H_{k}) = \left( \begin{pmatrix} n-(k-1) \\ 2 \\ \end{pmatrix} \right)^{-1}\]

So we have that

\[\begin{aligned} E( \sum_{k=1}^{n-1} H_{k}) &= \sum_{k=1}^{n-1} E(H_{k})\\ &= \sum_{k=1}^{n-1} \begin{pmatrix} (n-k+1)! \\ (n-k-1)! 2! \\ \end{pmatrix}^{-1} = \sum_{k=1}^{n-1} \frac{2(n-k-1)!}{(n-k+1)!}\\ &= \sum_{k=1}^{n-1} \frac{2}{(n-k+1)(n-k)} = \sum_{k=1}^{n-1} \frac{2}{k(k+1)}\\ &= 2 \left( 1 - \frac{1}{n} \right) \end{aligned}\]

Further, since $H_{n-1} \sim \text{Exp} \left(
\begin{pmatrix} 2
2
\end{pmatrix} \right)$

\[E(H_{n-1} ) = 1\]

Continuous-time Markov Chains

Some definitions

Definition 99. *A continuous-time process ${X_{t}}_{t \in [0,\infty )}$ satisfies the Markov property if

\[P(X_{t_{n}} = j \mid X_{t_1} = i_1, \ldots , X_{t_{n-1} } = i_{n-1} ) = P(X_{t_n} = j \mid X_{t_{n-1} } = i_{n-1} )\]

for all $j, i_1, \ldots , i_{n-1} \in E$ and for any sequence $0 \leq t_1 < \ldots < t_{n} < \infty$ of times (with $n \in \mathbb{N}$ )*

Definition 100. *The transition probability $p_{ij} (s,t)$ is, for $s \leq t, i,j \in E$

\[p_{ij} (s,t) = P(X_{t}= j \mid X_{s}=i)\]

also, the chain is homogeneous if

\[p_{ij} (s,t) = p_{ij} (0,t-s)\]

Write $p_{ij} (t-s) = p_{ij} (s,t)$ in this case
Let $\mathbf{P}{t} = (p{ij} (t))$*

Theorem 101. The family ${\mathbf{P}_{t} : t \geq 0}$ is a stochastic semigroup; that is, it satisfies

$\mathbf{P}_0 = I_{K\times K}$
$\mathbf{P}_{t}$ is stochastic - non-negative entries with rows summing to $1$
*The Chapman-Kolmogorov equations hold:
\[\mathbf{P}_{s+t} = \mathbf{P}_{s}\mathbf{P}_{t},\quad \forall s,t \geq 0\]

Definition 102. *The semigroup ${\mathbf{P}_{t}}$ is called standard if

\[\lim\limits_{t \downarrow 0} \mathbf{P}_{t} = \mathbf{I}\ (= \mathbf{P}_0 )\]

where $\mathbf{I} = \mathbf{I}{K\times K}$
A semigroup standard $\iff$ its elements $p{ij} (t)$ are continuous functions in $t$*

Holding times and alarm clocks

Holding times

Suppose that we have ${X_{t}}{t\geq 0}$ a continuous-time homogeneous Markov Chain, suppose that $t \geq 0$ and for, $i \in E$, we have $X{t}=i$. Given $X_{t}=i$, define

$H_{\mid i} = \inf \{s \geq 0 : X_{t+s} \neq i\}$ to be the holding time at state $i$ , that is the length of time that a continuous-time Markov chain started in state $i$ stays in state $i$ before transitioning to a new state.
Note that holding times does not depend on $t$ since we work under time-homogeneity assumption

\[\inf \{s \geq 0: X_{t+s} \neq i\}\mid X_{t} = i \stackrel{\text{def.}}{=} = \inf \{s \geq 0: X_{s} \neq i\}\mid X_0 =i\]

Theorem 103. The holding times $H_{\mid i}$, for $i \in E$ follows an exponential distribution

Describing the evolution of a Markov Chain using exponential holding times

Can describe the evolution of continuous-time Markov chains by specifying transition rates between states and using the concept of exponential alarm clocks

$\forall i \in E$ denote $n_{i}$- number of states which can be reached from state $i$
Associate $n_{i}$ independent, exponential alarm clocks with rates $q_{ij}$ provided $j$ can be reached from state $i$
When chain first visits state $i$, all $n_{i}$ exponential alarm clocks are set simultaneously
First alarm clock which rings, determines which state the chain transitions to.
As soon as state $j$ has been reached - set $n_{j}$ independent exponential alarm clocks associated to $j$and repeat the process
\[q_{ij} \text{ - \textbf{transition rates} }\]
Let $i \neq j$, with $q_{ij} > 0$ denote the transition rates when state $j$ can be reached from state $i$
Let $i \neq j$, set $q_{ij} = 0$ if $j$ can’t be reached from $i$
Also set $q_{ii} = 0, \forall i \in E$
The minimum/infimum of the $n_{i}$ exponential alarm clocks of state $i$,follows an exponential distribution with rate
\[q_{i} = \sum_{j\in E} q_{ij}\]
$P(i \to j) = P(q_{i} = q_{ij} ) = \frac{q_{ij} }{q_{i}}$
Hence, the transition probabilities of embedded chain $Z$ given by
\[p_{ij}^{Z} = \frac{q_{ij} }{q_{i}}\]
We assumed above that $0 < q_{i} < \infty$. In case that $q_{i} = 0$ then we have $p_{ii}^{Z} = 1$

The generator

Definition 104. *The generator $\mathbf{G} = (g_{ij} ){i,j \in E}$ of the Markov chain with stochastic semigroup $\mathbf{P}{t}$ is defined as the $card(E) \times card(E)$ matrix given by

\[\mathbf{G} := \lim\limits_{\delta \downarrow 0} \frac{1}{\delta }[\mathbf{P}_\delta - \mathbf{I} ] = \lim\limits_{\delta \downarrow 0} \frac{1}{\delta }[\mathbf{P} -\mathbf{P}_0]\]

That is, $\mathbf{P}_{t}$ differentiable at $t =0$*

Transition probabilities of the associated jump chain

Can now derive the transition probabilities of the embedded/jump chain - expressing them in terms of the generator
if $X_{t} = i$- stay at $i$ for exponentially distributed time with rate $-g_{ii} = q_{i}$ and then moves to other state $j$
Probability that the chain jumps to $j \neq i$ is $-g_{ij}/ g_{ii}$
i.e for $i \neq j$,

\[p_{ij}^{Z} = -\frac{g_{ij}}{g_{ii}} = \frac{q_{ij} }{q_{i}}\]

Equivalent to

\[q_{ij} = q_{i}p_{ij}^{Z}\]

The forward and backward equations

Theorem 105. *Subject to regularity conditions, a continuous-time Markov chain with stochastic semigroup ${\mathbf{P}_{t}}$ and generator $\mathbf{G}$ satisfies the Kolmogorov forward equation

\[\mathbf{P}^\prime_{t} = \mathbf{P}_{t}\mathbf{G}\]

and the Kolmogorov backward equation

\[\mathbf{P}'_{t}= \mathbf{G} \mathbf{P}_{t},\quad \forall t \geq 0\]

Matrix exponentials

Irreducibility, stationarity and limiting distribution

Definition 106. Chains is irreducible if for any $i,j \in E$ we have $p_{ij} (t) > 0,$ for some $t$

Theorem 107. If $p_{ij} (t) > 0, \text{ for some } t > 0$ then $p_{ij} (t) > 0,\ \forall t > 0$

Definition 108. *A distribution $\mathbf{\pi}$ is the limiting distribution of a continuous-time Markov chain if, for all states $i,j \in E$ we have

\[\lim\limits_{t \to \infty} p_{ij} (t) = \pi_{j}\]

Definition 109. A distribution $\mathbf{\pi}$ is a stationary distribution if $\mathbf{\pi = \pi P_{t}} \ \forall t \geq 0$

Theorem 110. Subject to regularity conditions, we have $\mathbf{\pi = \pi P_{t}}, \forall t \geq 0 \iff \mathbf{\pi G} = 0$

Theorem 111. Let $X$ an irreducible Markov chain with a standard semigroup ${\mathbf{P}_{t}}$ of transition probabilities

*If $\exists$ stationary distribution $\mathbf{\pi}$ then it is unique and $\forall i,j \in E$
\[\lim\limits_{t \to +\infty } p_{ij} (t) = \pi_{j}\]
*If there is no stationary distribution then
\[\lim\limits_{t \to +\infty} p_{ij}(t) = 0 \ \forall i,j \in E\]

Jump chain and explosion

Subject to regularity conditions, can construct the jump chain $Z$ from a continuous time Markov chain $X$ as follows

$J_{n}$ denote the $n$th change in value of the chain $X$ and set $J_0 = 0$
Values $Z_{n} = X_{J_{n}+}$ of $X$ form a discrete-time Markov Chain $Z = {Z_{n}}_{n \in \mathbb{N}_0}$
Transition matrix of $Z$ denoted by $\mathbf{P}^Z$ and satisfies
- $p_{ij}^{Z} = g_{ij} / g_{i}$ if $g_{i} := - g_{ii} > 0$
- if $g_{i} = 0$, then the chain gets absorbed in state $i$ once it gets there for the first time.
If $Z_{n} = j$ then the holding time $H_{n+1} = J_{n+1} -J_{n} = H_{\mid j}$ has exponential distribution with parameter $g_{j}$
The chain $Z$ is called the jump chain of $X$

Consider the converse - a discrete-time Markov chain $Z$ taking values in $E$ - Try and find a continuous-time Markov chain $X$ having $Z$ as its jump chain - Many such $X$ exist

Let $\mathbf{P}^Z$ denote transition matrix of the discrete-time Markov chain $Z$ taking values in $E$
Assume $p_{ii}^{Z} = 0,\ \forall i \in E$
$i \in E$ let $g_{i}$ denote non-negative constants. Define
\[g_{ij} = \begin{cases} g_{i}p_{ij}^{Z} , &\text{ if } i \neq j;\\ - g_{i} , &\text{ if } i = j. \end{cases}\]

Construction of continuous-time Markov chain $X$ done as follows

Set $X_0 = Z_0$
After holding time $H_1 = H_{\mid Z_0} \sim Exp(g_{Z_0})$ the process jumps to state $Z_1$
After holding time $H_2 = H_{\mid Z_1} \sim Exp(gZ_1)$ the process jumps to state $Z_3$
Formally: conditionally on the values $Z_{n}$ of chain $Z$ let $H_1, H_2, \ldots$ be independent random variables with exponential distribution $H_{i} \sim Exp(gZ_{i-1} )$, $i = 1,2, \ldots$. Set $J_{n} = H_1 + \ldots + H_{n}$
Then define
\[X_{t} = \begin{cases} Z_{n}, &\text{ if } J_{n} \leq t \leq J_{n+1} \text{ for some } n ;\\ \infty , &\text{ otherwise i.e. if } J_\infty \leq t . \end{cases}\]
Note that the special state $\infty$ added in case the chain explodes Recall that $J_\infty = \lim\limits_{n \to \infty} J_{n}\cdot J_\infty$ called the explosion time say chain explodes if
\[P(J_\infty < \infty ) > 0\]
Can show that
$X$ a continuous-time Markov chain with state space $E \cup {\infty }$
Matrix $G$ is the generator of $X$
$Z$ is the jump chain of $X$

Theorem 112. The cain $X$ constructed above does not explodes if any of the following conditions hold

State space $E$ is finite
$\sup_{i \in E} g_{i} < \infty$
$X_0 = i$ where $i$ a recurrent state for the jump chain $Z$

Birth processes

Definition 113. A birth process with intensities $\lambda_0, \lambda_1, \ldots \geq 0$ a stochastic process ${N_{t}}_{t \geq 0}$ with values in $\mathbb{N}_0$, such that

Non-decreasing process: $N_0 \geq 0$; if $s < t$ then $N_{s}\leq N_{t}$
*There is a ‘single arrival’ i.e. the infinitesimal transition probabilities are for $t \geq 0, \delta > 0, n ,m \in \mathbb{N}_0$
\[P(N_{t+\delta } = n + m \mid N_{t} = n ) = \begin{cases} 1 - \lambda_{n}\delta + o(\delta ), &\text{ if } m = 0 ;\\ \lambda_{n}\delta + o(\delta ), &\text{ if } m =1 ;\\ o(\delta ) &\text{ if } m > 1 \end{cases}\]
Conditionally independent increments: Let $s < t$ then the conditional on the values of $N_{s}$, the increment $N_{t}-N_{s}$ is independent of all arrivals prior to $s$

*Note that by conditionally independent increments, mean that for $0 \leq s < t$, conditional on the value of $N_{s}$, the increment $N_{t} - N_{s}$ independent of all arrivals prior to $s$ i.e. for $k,l , x(r) \in {0,1,2, \ldots }$ for $0 \leq r<s$ we have

\[P(N_{t} - N_{s} = k \mid N_{s} = l, N_{r} = x(r) \text{ for } 0 \leq r< s) = P(N_{t}-N_{s} = k \mid N_{s}= l)\]

Birth process a continuous-time Markov chain
A Poisson process a special case of a birth process (with $\lambda_{n} = \lambda , \forall n \in \mathbb{N}_0$)
With the general case, birth rates depend on the current state of the process.*

The forward and backward equations

Let ${N_{t}}$ a birth process with positive intensities $\lambda_0 ,\ldots$\, With transition probabilities

\[p_{ij} (t) = P(N_{t+s} = j \mid N_{s}= i ) = P(N_{t}= j \mid N_0 = i), \quad \text{for } i,j \in E\]

Theorem 114. *For $i,j \in E, i < j, t \geq 0$ the forward equations of a birth process are given by

\[\frac{dp_{ij}(t)}{dt} = -\lambda_{j}p_{ij} (t) + \lambda_{j-1} p_{i,j-1} (t)\]

with $\lambda_{-1} = 0,$ and the backward equation given by

\[\frac{dp_{ij} (t)}{dt} = -\lambda_{i}p_{ij}(t) + \lambda_{i}+p_{i+1,j} (t)\]

Where for both, boundary condition given by $p_{ij} (0) = \delta_{ij}$ - $\delta$ the Kronecker delta*

Theorem 115. Let ${N_{t}}_{t\geq 0}$ a birth process of positive intensities $\lambda_0, \ldots$ Then the forward equations have unique solutions which satisfies the backward equations

Explosion of a birth process

Definition 116. *Let $J_0, J_1, \ldots$ denote the jump times of a birth process $N$

\[J_0 = 0 \quad J_{n+1} = \inf \{t \geq J_{n}: N_{t}\neq N_{J_{n}} \}, \quad n \in \mathbb{N}_0\]

Further let $H_1,H_2, \ldots$ denote the corresponding holding times. As before, we write

\[J_\infty = \lim\limits_{n \to \infty} J_{n}= \sum_{i=1}^{\infty} H_{i}\]

Then we say that explosion of the birth process $N$ is possible if

\[P(J_\infty < \infty ) > 0\]

Theorem 117. Let $N$ be a birth process started from $k \in \mathbb{N}0$, with rates $\lambda{k},\lambda_{k+1}, \ldots > 0 $ Then:

\[\text{ If } \sum_{i=k}^{\infty} \frac{1}{\lambda_{i}} \begin{cases} < \infty , &\text{ Then } P(J_\infty < \infty ) = 1 \text{ (Explosion occurs with probability 1)} ;\\ = \infty , &\text{ Then } P(J_\infty = \infty ) = 1 \text{ (Probability explosion occurs is 0)} . \end{cases}\]

Birth-death processes

Definition 118. Birth-death process
Suppose we are given the following process ${X_{t}}_{t \geq 0}$

${X_{t}}_{t \geq 0}$ is Markov chain on $E = \mathbb{N}_0$
*The infinitesimal transition probabilities are (for $t \geq 0, \delta > 0, n \in \mathbb{N}_0, m\in \mathbb{Z}$ )
\[P(X_{t+\delta } = n+m \mid X_{t}=n ) =\begin{cases} 1 - (\lambda_{n}+ \mu_{n})\delta + o(\delta ), &\text{ if } m = 0 ;\\ \lambda_{n} + o(\delta ), &\text{ if } m = 1.\\ \mu_{n}\delta + o(\delta ), & \text{ if } m = -1\\ o(\delta ), & \text{ if } \left\vert m \right\vert >1 \end{cases}\]
*The birth rates $\lambda_0, \lambda_1, \ldots$ and the death rates $\mu_0, \mu_1, \ldots$ satisfy
\[\lambda_{i}\geq 0, \quad \mu_{i} \geq 0 \quad \mu_0 = 0\]

*We have the generator given by

\[\begin{pmatrix} -\lambda_0 & \lambda_0 & 0 & 0 & 0 & \ldots \\ \mu_1 & -(\lambda_1 + \mu_1) & \lambda_1 & 0 & 0 & \ldots \\ 0 & \mu_2 & -(\lambda_2 + \mu_2) & \lambda_2 & 0 & \ldots \\ 0 & 0 & \mu_3 & -(\lambda_3 + \mu_3) & \lambda_3 & \ldots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots\\ \end{pmatrix}\]

*We take a look at the asymptotic behaviour of the process.
Suppose that $\mu_{i}, \lambda_{i} > 0, \forall i$, where the rates make sense. Then using the claim $\pi G = 0$

\[\begin{aligned} -\lambda_0\pi_0 + \mu_1 \pi_1 &= 0\\ \lambda_{n-1} \pi_{n-1} - (\lambda_{n}+ \mu_{n})\pi_{n} + \mu_{n+1}\pi_{n+1} &= 0, \quad n \geq 1\end{aligned}\]

Brownian Motion

From random walk to Brownian motion

Modes of convergence in distribution, Slutsky’s theorem and the CLT

Definition 119. *(Convergence in probability)
A sequence of random variables $X_1, X_2, \ldots$ converges in probability to $X$ written $X_{n} \xrightarrow{P} X$ if for each $\epsilon >0$

\[\lim\limits_{n \to \infty} P(\{\omega : \left\vert X_{n}(\omega ) - X(\omega ) \right\vert \geq \epsilon \}) = \lim\limits_{n \to \infty} P(\left\vert X_{n}-X \right\vert \geq \epsilon) = 0\]

Definition 120. *(Convergence in distribution)
Let the cumulative distribution function of $X_{n}$ and $X$ be denoted by $F_{n}$ and $F$ respectively
Say $X_{n}$ converges in distribution/weakly to $X$, written $X_{n} \xrightarrow{D}X$ if

\[\lim\limits_{n \to \infty} F_{n}(x) = F(x), \quad \text{for every continuity point } x \text{of} F(x)\]

Theorem 121. *(Slutsky’s theorem)
Suppose that $X_{n}\xrightarrow[]{d} X, A_{n}\xrightarrow[]{P}a, B_{n}\xrightarrow[]{P}b$, where $a,b$ are (deterministic) constants. Then

\[A_{n}X_{n}+ B_{n} \xrightarrow[]{d} aX + b\]

Theorem 122. *(Central limit theorem)
Let $Z_1,Z_2, \ldots$ a sequence of i.i.d random variables of finite mean $\mu$ and finite variance $\sigma^{2}$. Then the distribution of

\[\frac{1}{\sigma \sqrt{n} } \left( \sum_{i=1}^{n} Z_{i} - n \mu \right)\]

tends to standard normal distribution as $n \to \infty$*

Brownian Motion

Definition 123. A real-valued stochastic process $B = {B_{t}}_{t \geq 0}$ a standard Brownian motion if

$B_0 = 0$ almost surely
$B$ has independent increments
$B$ has stationary increments
*The increments are Gaussian, for $0 \leq s < t$
\[B_{t} - B_{s} \sim N(0,(t-s));\]
The sample paths are almost surely continuous i.e. the function $t \mapsto B_{t}$ almost surely continuous in $t$

Definition 124.*Let $B = {B_{t}}{t \geq 0}$ denote a standard Brownian motion.
Stochastic process $Y = {Y{t}}_{t \geq 0}$ defined by

\[Y_{t} = \sigma B_{t} + \mu_{t}, \forall t \geq 0\]

is called a Brownian motion with drift parameter $\mu \in \mathbb{R}$ and variance parameter $\sigma^{2} , \sigma > 0$
Note for $0 \leq s < t, Y_{t} - Y_{s} \sim N(\mu (t-s), \sigma^{2} (t-s))$*

Finite dimensional distributions and transition densities

Theorem 125. *Let $f\colon \mathbb{R} \to \mathbb{R}$ a continuous function satisfying some additional regularity conditions. Then the unique (continuous) solution $u_{t}(x)$ to the initial value problem

\[\begin{aligned} \frac{\partial }{\partial t} u_{t}(x) &= \frac{1}{2} \frac{\partial^{2} }{\partial x^{2} }u_{t}(x)\\ u_0(x) &= f(x) \end{aligned}\]

is given by

\[u_{t}(x) = E[f(W_t^{x})] = \int_{-\infty}^{\infty} p_t (x,y) f(y) \,\mathrm{d}y\]

where ${W_{t}^x}$ is a Brownian motion started at $x$*

Symmetries and scaling laws

Proposition 126. Let ${B_{t}}_{t \geq 0}$ a standard Brownian motion. Then each of the following processes is also a standard Brownian motion

${-B_{t}}_{t \geq 0}$		Reflection
${B_{t+s} - B_{s}}_{t \geq 0}$	for $s \geq 0$	Translation
${aB_{t/ a^{2} }}_{t \geq 0}$	for $a \geq 0$	Rescaling (Brownian scaling property)
${tB_{1 / t}}_{t \geq 0}$		Inversion

Some remarks

First look at maximum and minimum processes

\[\begin{aligned} M_t^+ &:= \mathop{\max} \{B_{s} : 0 \leq s \leq t\}\\ M_t^- &:= \mathop{\min} \{B_{s} : 0 \leq s \leq t\}\\\end{aligned}\]

These are well-defined, because the Brownian motion has continuous paths, and continuous functions always attain their maximal and minimal values on compact intervals
Observe that if the path $B_{t}$ is replaced by its reflection $-B_{t}$ then the maximum and the minimum are interchanged and negated
Since $-B_{t}$ a Brownian motion, follows that $M_t^+, -M_t^-$ have same distribution

\[M_t^+ \stackrel{d}{=} -M_t^-\]

As a first example, consider implications of Brownian scaling property for the distributions of the maximum random variables $M_t^+$ . Fix $a > 0$ , and define

\[\begin{aligned} B_t^{\ast} &:= a B_{t/a^{2} } \\ M_t^{+,\ast} &:= \mathop{\max}_{0 \leq s \leq t}B_s^{\ast} \\ & = a M_{t/a^{2}}^{+} \end{aligned}\]

By Brownian scaling property $B_t^{\ast}$ is a standard Brownian motion, and so random variable $M_t^{+ \ast}$ has same distribution as $M_{t^+}$. Therefore

\[M_t^+ \stackrel{d}{=} a M_{t/a^{2} }^+\]

Can be shown, above implies that the sample paths of a Brownian motion are with probability one, nowhere differentiable

The reflection property and first-passage times

Proposition 127. *Let $x > 0$ then

\[P(M_t^+ \geq x) = 2P(B_{t} > x) = 2 -\Phi (x / \sqrt{t} )\]

Where $\Phi$ the normal c.d.f*

A model for asset prices

A model for describing movement of an asset price ${S_{t}}{0 \leq t \leq T}, S{t} \in \mathbb{R}^+$ is as follows

\[S_{t} = S_0 \exp \{ (\mu -\sigma^{2}/2)t + \sigma B_{t}\}\]

where $S_0$ the initial value of the underlying stock. $\mu \in \mathbb{R}$ is the risk-free interest rate and $\sigma$ the volatitily (the instantaneous standard deviation of the stock)
This process known as geometric Brownian motion.
It is well-known that this model does not fit the stylized features of financial returns data.
Real financial data does not follow the dynamic above; because in practice volatility of asset prices is typically not constant, and often responds to a variety of market conditions
We typically observe time-varying volatility clusters.
This has yielded much academic and industrial research into cases (which goes back to at least the late 1970s) where $\sigma$ is a stochastic process, e.g:

\[\begin{aligned} S_{t} &= S_o \exp \left\{ \left( \mu t - \frac{1}{2} \int_{0}^{t} \sigma^{2}_{s} \,\mathrm{d}s + \int_{0}^{t} \sigma_{s} \,\mathrm{d}B_{s} \right) \right\}\\ \sigma_{t}&= \sigma_0 \exp \{\gamma t + \eta W_{t}\} \end{aligned}\]

where $W_{t}$ is an independent Brownian motion; such a model is termed a stochastic volatility model\